Group Activity:
Square and Cubic Units

Length, Area, and Volume

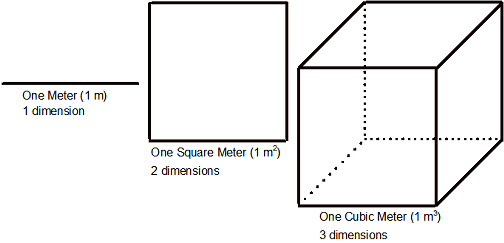
The SI units of area and volume are the square meter (m²) and the cubic meter (m³). They are called derived units because they are built up from simpler units. In the image below the differences between length, area and volume units are made clear. To measure a length requires just one dimension, one measurement. To measure area requires two dimensions: two lengths multiplied together. To measure volume requires three dimensions: three lengths multiplied together.

To convert from one unit of area or volume to another can be done in two ways. First, the length conversion factor can be used to make a new conversion factor for area or volume. Second, the length conversion factor can be used more than once: twice for area units and three times for volume units.

Making Conversion Factors

Here is how to do this, step-by-step:

1. Write out the full conversion factor for converting length (for ex., 1 ft = 12 in).
2. For area, square both sides of the equation. For volume, cube both sides of the equation.
3. Be sure to square or cube the unit in addition to the number.

1 ft = 12 in                    1 mi = 5,280 ft 
(1 ft)2 = (12 in)2              (1 mi)2 = (5,280 ft)2
1 ft2 = 144 in2                 1 mi2 = 2.78784 × 107 ft2
Now that you have a conversion factor, use it:
         144 in2
2 ft2 × --------- = 288 in2
          1 ft2

1 m = 100 cm                    3 ft = 1 yd 
(1 m)3 = (100 cm)3              (3 ft)3 = (1 yd)3 
1 m3 = 1 × 106 cm3              27 ft3 = 1 yd3
Now that you have a conversion factor, use it:
         1 × 106 cm3
3.5 m3 × ----------- = 3.5 × 106 cm3
            1 m3        

Using Conversion Factors More than Once

Here is how to do this, step-by-step:

1. Write the number to be converted with its unit.
2. If the unit is squared then write the conversion factor for length twice, being sure that the units to be cancelled are on the opposite sides of the fraction bar.
3. If the unit is cubed then write the conversion factor for length three times, being sure that the units to be cancelled are on the opposite sides of the fraction bar.

Convert cm2 to m2:
               1 m       1 m
45,000 cm2 × ———————— × ———————— = 4.5 m2
             100 cm      100 cm

Convert m3 to ft3
         3.28 ft   3.28 ft   3.28 ft
5.2 m3 × ——————— × ——————— × ——————— = 183 ft3
           1 m      1 m        1 m

Do your work on a separate piece of paper, being sure to label each problem clearly. To do these problems you may need your conversions chart from the original dimensional analysis packet and your metric units chart.

Create Conversion Factors

Create conversion factors between the two units given in each problem.

Do Some Conversions

Perform the following conversions, showing all work.

21. One square mile contains 640 acres. How many square feet are there in an acre?
22. A unit commonly used in teaching organic chemistry in the lab is the microliter (μL). Express the volume of this unit using a unit derived from metric length units. Set up a conversion factor so that 1 μL = 1 of the new unit. Hint: Start with the fact that 1 mL is defined as 1 cm³.