Circular Orbit

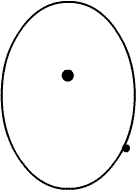
Elliptical Orbit

Planetary Orbits:
Not a Perfect Circle

Background Information

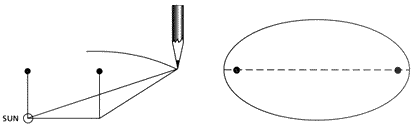
Pictures of the Solar System tend to show all the orbits of the planets as circles centered on the Sun (see image at left). The big object in the center of the circle represents the Sun. The smaller object on the circle represents a planet. Notice that the Sun is exactly in the center of the orbit. No orbit in the solar system is perfectly round.

In reality, the planets orbit the Sun travelling along an oval path (see image at right). The mathematical term for this shape is an ellipse. This ellipse is a little more stretched out than real planetary orbits but it has been exaggerated on purpose to demonstrate the shape more clearly. Notice that the Sun in this picture is not right in the center. The Sun is at one of the two ‘centers’ of the ellipse. These are called foci (plural for focus). The closer these foci are together, the more circular the orbit. The orbit of Venus is the closest to a circle of any planet in the Solar System. Scientists have a name to describe just how much like an ellipse an orbit is. This is called eccentricity and is a measure that uses numbers between 0 and 1. If an orbit has an eccentricity close to 1 then the ellipse is so long as to be more cigar-shaped than round. Comets tend to have very elongated, high-eccentricity orbits. The closer the eccentricity is to zero, the more circular the orbit.

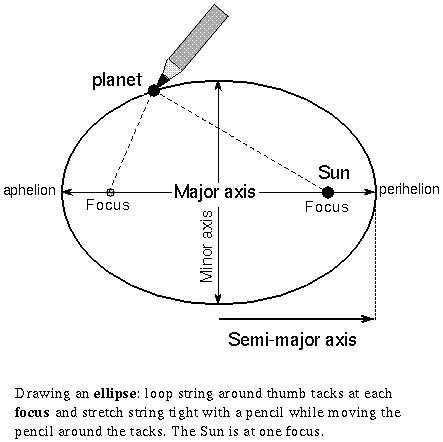
In the image at right you can see some of the vocabulary words you need in order to understand ellipses. The ellipse itself is the big oval shape. It has two axes: a major axis (the longer axis) and a minor axis (the shorter one). It has two foci: in the case of planetary orbits one focus is the Sun. All the points in an ellipse are defined in relation to the foci. The sum of the distances from each point on the ellipse to both foci is constant for all points on the ellipse. The point on an orbit nearest the Sun is called perihelion. The point farthest from the Sun is called aphelion.

Eccentricity is a measure of how round or elongated an ellipse is. It is calculated by dividing the distance between the foci by the length of the major axis.

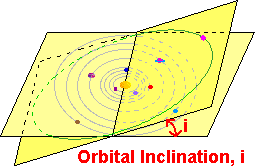
One other unrelated thing you should know is that the planets are not all on the same plane. Imagine the Solar System as a giant disk defined by the Earth’s orbit. All of the planets’ orbits are sometimes above this disk and sometimes below it. Astronomers say that the orbits of the planets have different inclinations relative to Earth’s orbit. The ecliptic is the astronomer’s word for this giant disk. In our sky we see the disk as a line that circles the Earth. It can also be understood as the apparent path of the Sun through the sky as the Earth orbits it. Because the planets are usually above or below this disk we call the ecliptic they appear above and below the line of the ecliptic in the sky.

Drawing Ellipses

This experiment will demonstrate the relationship between the distance between the foci of an ellipse, the length of the major axis, and the eccentricity of the ellipse. You will learn how planets really move in their orbits. You will speculate on what life would be like on a planet with a very elliptical orbit and on whether life would even be possible there.

Materials

• One piece of cardboard
• Two pins or thumbtacks
• Colored pencils
• A piece of paper
• Several lengths of string
• Scissors
• A ruler
• A calculator

Procedure

1. Place a piece of paper on top of the cardboard so the long dimension runs from left to right. From the top left corner, measure down half of the width of the paper, then measure to the right 10 cm. Mark this point with a dot, push a pin through the dot into the cardboard, and label it “Sun.” Do not move this pin during the rest of the experiment.
2. Refer to the data table on the next page. Position the second pin the correct distance to the right of the Sun to represent the second focus for that planet. Note: The pins do not represent the planets—they are only the second focus of the ellipse. You will use it to help you draw that planet’s orbit. You will do this for each planet in turn.
3. In the data table you will see that each planet, in addition to the distance between its pins, also has a value for the length of the loop of sting you will use to help you draw its orbit. Measure out a length of string that is 4 cm longer than the distance given. This gives you 2 cm at each end to make a knot in the string. Make a knot in the string to make a loop with a circumference equal to the distance given in the table.
4. Place the string loop around both pins. Put a colored pencil inside the loop. Use a different color for each planet. Move the pencil so that the string forms a triangle around the pins and the pencil point as shown in the diagrams. To draw an orbit, keep the pencil on the paper inside the string loop. Keep the string tight with the pencil and move the pencil around the pins.
5. Label each loop with the name of the planet given.
6. Right after you finish drawing each loop, measure the major axis of the ellipse and enter it in the data table. The major axis is the line that runs from one end of the ellipse to the other right through the two pins at the foci.
7. Calculate the value of the eccentricity of the orbits you
   (D_f) ÷ (L_a) = E
   have drawn by using the formula shown at right. The formula says that you divide the distance between the foci (D_f) by the length of the major axis (L_a) to get the value of ‘E’ for eccentricity. Enter this data in the table.
8. This sheet of paper with your ellipses is a required part of this assignment and must be turned in with the questions you will find on the next page.

Ellipses Questions

In the table above you will find data about the planets in our Solar System. They are in order by their eccentricities. Compare the values you found for the experimental eccentricites to the values of the planets in our Solar System. Use this data and the data you collected to create a graph. Graph paper has been provided. Along the bottom write the names of the planets, including the made-up planets. Space them equally on the long axis of the graph paper. Along the left side make a scale for the eccentricity. It should range from 0 to 1. You will make a simple bar graph that helps you to see the differences in the value of the eccentricity for different planets. Use the graph of the data you collected to help you answer the following questions.

1. What is the shape of the most eccentric orbits? What is the shape of the least eccentric orbits?
2. Which of the real planets are the most eccentric? (name three)
3. Which of the made-up planets are the most eccentric? (name three)
4. If you were to add another orbit to your diagram and you wanted to draw a planet with an eccentricity value of 0.90, how far apart would the foci be if the major axis measures 27.0 cm?

Use your imagination to answer these questions. Imagine that the Earth had a much higher eccentricity (say around 0.40). At some times of the year we would be very close to the Sun and at other time we would be very far away. Perihelion and aphelion would be at very different distances from the Sun. An important fact is that the farther from the Sun a planet is, the slower it moves. This means that we would be in the cold far-from-the-Sun part of the orbit longer than in the hot close-to-the-Sun part of the orbit.

5. Describe what it would be like to live on a planet with such a high eccentricity. Draw an ellipse with the right eccentricity and use it to imagine how the amount of sunlight would change from perihelion (closest approach to the Sun) to aphelion (farthest point from the Sun). This drawing is required in order to receive full credit for this question. Suggestion: use a major axis of 15 cm, a foci spacing of 3 cm and a loop of length 21 cm.
6. Imagine that this world has no tilt to its axis relative to its orbit. Would there be seasons on this planet? Explain your answer.
7. Earth’s orbit is very nearly circular with its eccentricity of 0.0167. Life is abundant on Earth. Form an opinion about life on a planet with high eccentricity. If you think life would be possible then explain why. If not, explain why not.

Comets have orbits with very high eccentricities. They originate in a zone far beyond the orbit of Pluto know as the Kuiper Belt. It is very like the Asteroid Belt found between the orbits of Mars and Jupiter. Kuiper Belt object are typically made of water ice, ammonia, methane and a little rock and metal. They are essentially dirty snowballs. Occasionally a passing star or other disturbance causes some of these objects to be accelerated toward the Sun. Since they originate from so far away their orbits are very elongated. Halley’s Comet (due to return to view on Earth in 2061) has an orbital eccentricity of 0.9673. Its orbit is inclined 163° to the ecliptic. The orbital period is 76 years.

8. The major axis of the orbit of Halley’s Comet is 35.88 AU. Given its eccentricity of 0.9673 how far from the Sun is the second focus of the orbit of Halley’s Comet? (Give your calculation in units of AU. An AU (Astronomical Unit) is the standard distance of the Earth from the Sun, about 93,000,000 miles.