Chemical Kinetics:
Reaction Rates

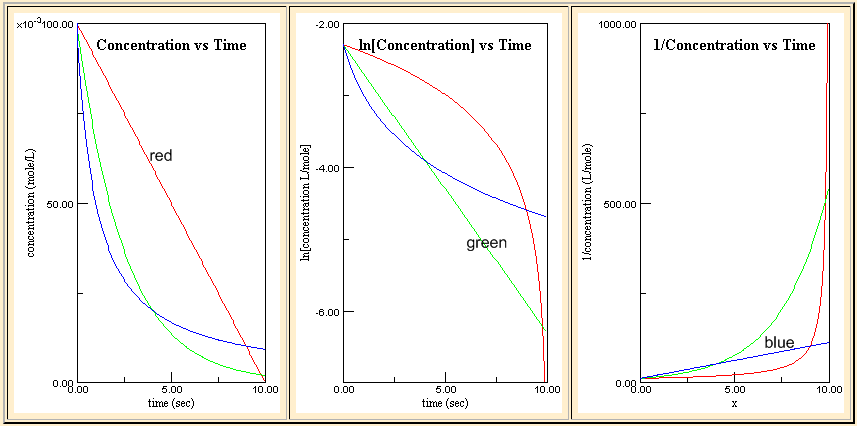
Reaction Order	Differential Rate Law	Integrated Rate Law	Linear Form	Characteristic Kinetic Plot	Half-life Expression	Units of Rate Constant
Zero	- d [A] d t = rate = k	[A] = [A]0 - k t	[A] = -k t + [A]0	[A] vs t	t½ = [A]0 2k	mole L-1 sec-1
First	- d [A] d t = rate = k [A]	[A] = [A]0 e- k t	ln[A] = -kt + ln[A]0	ln [A] vs t	t½ = ln(2) k	sec-1
Second	- d [A] d t = rate = k [A]2	[A] = [A]0 1 + k t [A]0	1   [A] = k t +   1   [A]0	1/[A] vs t	t½ =   1   k[A]0	L mole-1 sec-1

The series of three graphs shown below illustrate the use of the characteristic kinetic plots. The graph on the left shows [A] vs t plots for a zero-order (red line), first-order (green line), and second-order (blue line) reaction. The graph in the middle shows ln [A] vs t plots and the graph on the right shows 1/[A] vs t plots for each reaction order.