Student Worksheet for the Demonstration:
The Empirical Formula of Silver Oxide

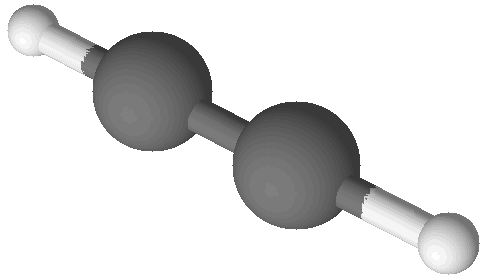
There are millions of chemical compounds described in the scientifc literature. In order to classify and organize all of these different substances it’s necessary to specify the their elemental composition. References of chemical compounds list their properties along with a chemical formula showing how many atoms of which elements make up individual molecules of that compound. How are these formulas determined?

While there are a large variety of modern, highly technological methods for determining the formulas of molecules (such as NMR) there is a tried and true method for doing it, too. The idea is simple enough: break a compound down into its elements, count the atoms of each element, and calculate a ratio in terms of whole numbers. For example, in order to determine the formula of the flammable gas known as acetylene one could burn it and collect the carbon dioxide and water vapor that results. Since acetylene is composed of only carbon and hydrogen it’s possible to count the atoms of carbon in the carbon dioxide and the atoms of hydrogen in the water to find out about the acetylene that was burned. When this is done the ratio of atoms is found to be 1 C for every 1 H. This is commonly written as a chemical formula: CH.

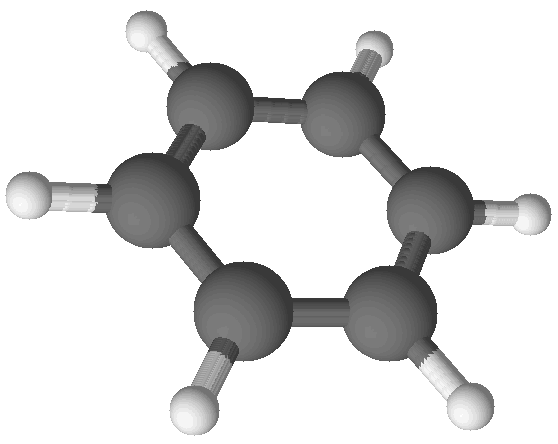
Benzene (C6H6)

Acetylene (C2H2)

The same procedure can be used for other compounds, such as benzene. Benzene is physically and chemically distinct from acetylene as it is a poisonous liquid which evaporates to make a flammable vapor. And yet when its formula is determined as described above it is found to also be CH. So it appears that two compounds have the same formula!

It turns out these two compounds have the same lowest-whole-number-ratio of atoms but they have different molecular structures. Both benzene and acetylene are shown in images at right. There are many hydrocarbon compounds that have the same ratio of carbon and hydrogen atoms but which have different chemical and physical properties. This is because these compounds have different numbers of atoms in their molecular structures. Acetylene and benzene have the same empirical formula, which is a formula with the lowest whole number ratio of atoms in the compound. These compounds have different molecular formulas, which give the true number of atoms in each molecule of the substance.

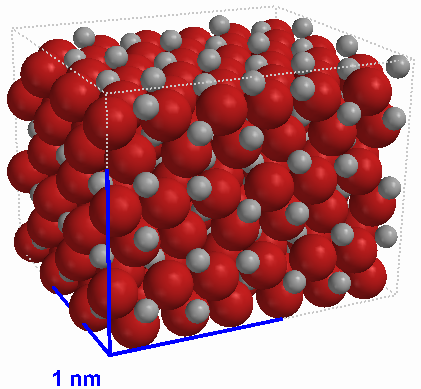
iron(III) oxide (Fe2O3) crystal

Some combinations of elements have one or more possible ratios but all samples with the same empirical formula are the same substance. For example, iron and oxygen form two main compounds: iron(II) oxide (FeO) and iron(III) oxide (Fe₂O₃). There are no compounds with the formula Fe₂O₂ or Fe₄O₆. This is because these compounds are ionic in nature, that is, they are composed of a specific ratio of two oppositely charged ions. As a result, they have two types of smallest particle, not just one as molecular compounds do. In the solid state such compounds form a repeating pattern in three dimensions called a crystal lattice. There is an image of the lattice of iron(III) oxide at left. Throughout the structure the ratio of positive ions to negative ions is the same. Ionic compounds are defined only in terms of the lowest whole number ratio of the ions of which they are composed. In other words, ionic compounds have only an empirical formula and do not have a molecular formula.

In this demonstration your teacher will show you a method by which the empirical formula of silver oxide may be found. Silver oxide will decompose on heating to form silver metal and oxygen gas. By carefully weighing a sample, placing it in a crucible, heating it over a bunsen burner, and weighing the resulting metal it will be possible to determine the ratio of silver to oxygen atoms in the original compound.

1. Use the data in the table at right to calculate the amount of iron oxide produced by rusting the steel wool. Also, calculate the amount of oxygen added to the steel wool in the formation of the iron oxide. (The data were generated by rapidly rusting steel wool, which is a form of iron. Rusting is a result of combination with oxygen.)

2. Calculate the moles of iron from the mass of the steel wool. Also, calculate the moles of oxygen atoms from the mass of oxygen you calculated in the previous step.
3. Calculate a ratio of moles of oxygen to moles of iron. Convert this ratio to a ratio of whole numbers.
4. Write the chemical formula of iron oxide based on your calculations. Also, write a balanced chemical equation for the reaction of iron with oxygen to form this compound.

5. As the demonstration proceeds, record the data in the table at right. Use the data to calculate the mass of silver oxide, the mass of silver at the end of the experiment, and the mass of oxygen that was driven off in the decompostion reaction.
6. Calculate the moles of silver and the moles of oxygen. Use these numbers to calculate a molar ratio for mol Ag/mol O in whole numbers.
7. Write the chemical formula of silver oxide based on your calculations. Also, write a balanced chemical equation for the decomposition of silver oxide to form oxygen and silver.
8. In your own words, define the terms empirical formula and molecular formula.
9. In your own words, explain why ionic compounds have empirical formulas but not molecular formulas.