Entropy and Probability

Over the course of this demonstration and class discussion students should begin to develop the following understandings.

1. Students will understand entropy as the tendency of matter and energy to assume the most probable arrangement.
2. Students will understand that the most probable arrangement is spread out, not concentrated.
3. Students will understand the idea that a given macrostate can have many microstates. The most probable macrostate is the state with the largest number of possible microstates.
4. Students will understand that spontaneous changes occur when entropy increases, that is when the number of available microstates increases. This process is driven by random motion and not by some additional force.

This document is to guide a teacher in carrying out this demonstration and is not a student handout.

Open and run the simulation found at this link: https://phet.colorado.edu/en/simulation/reversible-reactions. The direct link to the simulator is:https://phet.colorado.edu/sims/ideal-gas/reversible-reactions_en.jnlp. Make sure it works on your computer because it is Java-based. You will need a current version of Java.

Introduction: Some events occur spontaneously: ice melts in a room above 0°C, eggs break when dropped, and iron rusts. Ice can’t freeze above 0°C, eggs don’t jump up and reassemble and iron doesn’t un-rust. We are going to explore why some events are spontaneous and others are not.

Set up a vacuum pump or aspirator and connect it to a filter-flask with a stopper. Pump air out of the flask and ask students:

Walk around and read some student responses. Lead a discussion by eliciting their responses. Common responses will include that the air is sucked into or pushed into the flask. Students will not know what forces makes this happen. Move on to the next part of the demonstration without providing a final explanation as we will build one by the end.

Show the simulator on the overhead screen. Arrange it to have the barrier at its highest and to start with two particles on the left side. Ask students:

Next, we will consider the relevance of probability to the behavior of the particles. Ask students to draw all the possible arrangements of two particles, A and B, in the two boxes. There should be one arrangement with both on the left, two arrangements with one in each box, and one with both on the right. Click on the image below to open it in another browser window so it can be shared with students without showing this text.

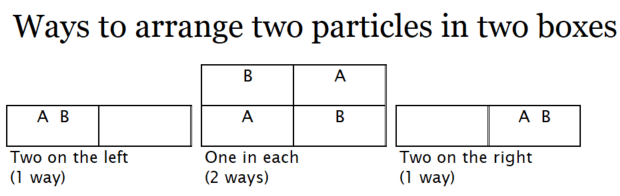
Ask students:

It is (1/2)²

Again (1/2)²

It is (1/2)¹

This is because there are two ways to have one on each side and only one way to have both on the right or both on the left.

Next we will look at a situation that has more particles. Set up the simulator to have four particles together on the left with the barrier all the way up. Ask students to predict what will happen and then:

The solution is below. After students work on it for a bit (it can be a bit of a challenge) show the image.

It is 1/16 for each four-in-one, 1/4 for each three-in-one, and 3/8 for the two-in-each. There are six ways to have two on each side so this is the most common arrangement. In the terminology used in this area of study, this is described by saying that there are six microstates in which there are two particles in each box. The two particles on each side arrangement is called a macrostate. Although we labeled the particles they would in reality be indistinguishable. So all six of these states are actually all exactly the same. When there are mutliple ways to arrange the same situation, or macrostate, those ways are called microstates. Systems naturally arrange themselves in a macrostate which has the maximum number of microstates, not because there is something forcing them to do so but simply because those macrostates are the most probable.

Set up the simulator with fifty particles on the left side with the barrier all the way up.

Lower the barrier and watch. Then repeat the exercise with all fifty starting on the right side. Fifty on the left and fifty on the right are macrostates which have just one microstate each. They are very unlikely. The probability is (1/2)⁵⁰.

There are 1.26 x 10¹⁴ microstates with 25 particles on each side. There is a 1 in 560 trillion chance of having all fifty particles on one side or the other. There is an 11% chance that there will be 25 on each side. There is an 88% chance of having between 20 and 25 on each side. There is a 99.87% chance of having between 15 and 25 particles on each side. It is much more likely to have an even distribution than a lopsided one.

Fifty particles is actually a very small number in the world of chemistry. Even a thousand or a million is a small number. Without collecting answers allow students to think about how many microstates there are that are evenly distributed for a million particles vs. the one microstate in which they are all on one side. The real power of this idea comes when students are confronted with a mole of particles. The chances of an uneven arrangement then become so small as to be unimaginable. Macrostates with very few or only one microstate are very low probability and are described as having low entropy. Macrostates with many microstates have a high probability and have a higher entropy. Natural systems proceed to change in such a way as to increase their entropy.

Probability favors the macrostate in which particles can have the maximum number of possible microstates. When particles are bunched up on one side there is only one way for this to happen, one microstate. When they are spread out there are many, many ways

The air rushes into the flask because the random motion of air molecules outside the flask made it possible for them to get inside and there are many more microstates available with more molecules in the flask than there are with only a few. If there are two areas near to one another and particles can pass between them then the particles will spread out to occupy both areas.

Air doesn’t rush back out of the flask because it is so unlikely for there to be all the air particles outside and a few or none inside. There is only one microstate in which the flask is completely empty, for example. Of all the possible arrangements this is surely the least likely.

There is no force necessary. The air particles are in constant motion. When they meet the opening in the flask there is less resistance (in the form of particles pushing them back) and so particles easily enter the flask. They enter quickly because air molecules move at an average speed of close to 1,000 mi/hr. They enter the flask until there are as many particles going in as coming out. This is the macrostate with the largest number of microstates: all of the air molecules in the room could take their turns inside the flask!

A process is spontaneous when there is an increase in entropy. If a process involves a decrease in entropy then it might not be spontaneous.

This demonstration is based in part on work produced by Ted Clark and Julia Chamberlain. It is published here: https://phet.colorado.edu/en/contributions/view/3948