In this lab students will measure the heat capacity of a coffee-cup calorimeter and use it to measure the molar heat of solution of potassium nitrate.
The scientific concept of energy is a difficult one. The basic idea is that energy is the capacity to do work or to oppose natural forces such as gravity or electric fields. This seems natural enough but what makes energy a difficult idea is that it is a mathematical abstraction which always has the same value. No matter what happens, the amount of energy involved in an event is always the same after the event as it was before the event. In fact, the amount of energy in the entire universe is understood to be constant. Formally, this idea is called the First Law of Thermodynamics. As in any measurement of the exchange of energy we will use this law in order to understand and interpret our work in the lab.
The trouble with the First Law is that it says nothing about what forms energy may take. We all have plenty of experience with identifying various forms of energy. For example, we all know that heat is a form of energy. Formally, the definition of heat is energy which when added to a system causes the random motion of its molecules to increase. Similarly, we know that light is either a form of energy or is an energy-delivery process: when you sit out in the sun you can feel your skin become warmer and heat is certainly a form of energy. Also, perhaps from other science classes, we know that energy can be associated with motion, so-called kinetic energy. The faster something is moving, the more energy it is understood to have. Finally, in another invention of scientists designed to keep track of this slippery abstraction, there is the concept of potential energy. One form of potential energy is called gravitational potential energy and can be understood through the following example. A 1 kg rock raised one meter above the floor will strike the floor at nearly 10 mph (4.4 m/s) when dropped. The same rock when dropped from 10 meters above the floor will strike at nearly 30 mph (14 m/s). Clearly the rock had more energy—potential energy—when raised to 10 m than when it was only 1 m above the floor.
Because energy is understood to have many forms it can be a difficult thing to measure and keep track of for purposes of making measurements of changes in energy. If energy should assume a form that you did not anticipate you may find that some energy is apparently lost. Fortunately in this lab activity the work is designed so that all energy will be in the form of heat. Even so, some careful thinking is involved in keeping track of the origins and destinations of the heat in this lab. We will use the First Law as follows: The heat lost by one object is gained by the others in contact with it. We will measure these exchanges of heat by way of measuring temperature. Heat itself is not directly measurable and there is no such thing as a ‘heatomometer’. Fortunately, there is such a thing as a thermometer.
In common speech heat and temperature are often interchangeable. “It’s cold in here, turn up the heat,” is equivalent to, “The temperature is too low in here, raise the temperature”. For this reason it can often be difficult to keep these ideas distinct from each other in the minds of students learning about energy. The concept of temperature is best understood as a measure of the average speed of molecular motion. The higher the temperature, the faster the molecules are moving and vice versa. The concept of heat is closely related: adding heat to a collection of molecules will cause their random motion to increase—the molecules will move faster on average than they did before heat was added. Taking heat away (cold is not considered a form of energy and therefore cannot be added) causes the average molecular speeds to be reduced. So adding heat raises temperature and removing heat reduces temperature.
There is a well-defined relationship between heat and temperature and it is known as the Zeroth Law of Thermodynamics. In the late nineteenth century a physicist named James Clerk Maxwell made some important contributions to our understanding of heat:
Discussing the concept of temperature, James Clerk Maxwell in 1872 wrote: “If when two bodies are placed in thermal communication, one of the two bodies loses heat, and the other gains heat, that body which gives out heat is said to have a higher temperature than that which receives heat from it.” He drew the corollary “If when two bodies are placed in thermal communication neither of them loses or gains heat, the two bodies are said to have equal temperatures or the same temperature. The two bodies are then said to be in thermal equilibrium.”
—Zeroth Law of Thermodynamics. 4 November 2011 19:58. Wikipedia. Accessed 11/18/2011. <http://en.wikipedia.org/wiki/Zeroth_law_of_thermodynamics>.
In essence what Maxwell was trying to say is that when you put a hot object next to a cold object the heat will flow from the hot to the cold until they have the same temperature. In this lab you will put some hot water into some cold water. The heat from the hot water will heat up the cold water. In the process the hot water loses heat. The First Law gives us to understand that the heat lost by the hot water equals the heat gained by the cold water. Another way to say this is to say that the sum of heat gained (a positive value) and the heat lost (a negative value) is zero:
Heat is calculated mathematically based on the change in temperature of a substance, the mass of the substance, and a quantity called the specific heat of the substance. The specific heat (also called heat capacity) is a constant that quantifies the amount of heat required to raise the temperature of one gram of a substance by 1 degree (°C or K). Actually, the specific heat is a function of temperature but for purposes of this lab we will assume that it is in fact constant over the temperature range we will encounter. The specific heat of water is 4.184 J/g·°C. Heat energy will be measured in joules (J) in this lab because J is the SI unit of energy. An older unit of energy is the calorie and it originates in the idea of specific heat since in units of calories the specific heat of water is 1 calorie/g·°C. This calorie is 1,000 times smaller than the Calories you are meant to fear as displayed on the Nutrition Facts labels on your food. Those Calories are really kilocalories. Specific heat will be denoted as a lower-case letter ‘s’. By comparison with water, many other substances have much lower specific heats. Copper, for example, has a specific heat of 0.385 J/g·°C. In effect, much less energy is required to raise the temperature of copper, per gram, than to raise the temperature of an equal mass of water.
There is a simple equation that we will use to calculate the amount of heat involved in a change in temperature. It is the product of the mass of the substance, the specific heat, and the change in temperature. The change in temperature is usually written as ΔT and is defined as the final temperature minus the initial temperature: ΔT = Tfinal – Tinitial. So heat is calculated as follows for 1.00 × 102 g of water that experiences a rise in temperature from 25.0°C to 45.0°C:
This shows the amount of heat required to raise the temperature of 100 g of water by 20°C. If the substance had been copper instead the same temperature rise would have required only 770 J. Alternatively, if the 8.37 kJ had been used to heat 100 g of copper the temperature change would have been much greater: ΔT = 227°C! Now let’s see how this discussion applies to establishing the final temperature upon mixing two masses of water at different temperatures (as you will do in this lab).
A calorimeter is made using two nested styrofoam cups and filled with 25.0 g of water at an initial temperature of 25.0°C. The initial temperature of the calorimeter is then also 25.0°C. A quantity of water is heated to 50.0°C and 25.0 g of this hot water is added to the calorimeter. What is the heat capacity of the calorimeter if the final temperature is 35.0°C?
First, let's take the point of view that the calorimeter is a perfect insulator and absorbs no heat from the hot water. It makes sense then that equal volumes of water at different temperatures will reach a temperature halfway between their initial values when they reach equilibrium. Specifically, 25.0 g of water at 25.0°C mixed with 25.0 g of water at 50.0°C will have an equilibrium temperature of 37.5°C. Even so, let's calculate this.
Ti = 25.0°C for the water in the calorimeterNow let’s come back to reality. Some of the heat from the hot water will go toward warming up the calorimeter and not the cold water. The actual final temperature will therefore be less. So we re-write the equation with this in mind:
qhot + qcold + qcalorimeter = 0In the study of the exchange of energy (a.k.a., Thermodynamics) a useful distinction is made between processes that release energy and those that absorb energy. When the system releases energy into the surroundings the process is called exothermic. This is readily observable as it causes a rise in temperature in both the system and the surroundings. In some cases, as in the case of heated water causing something else to get warm (for example, a hot cup of coffee spilling onto your lap) the energy released into the surroundings was clearly already in the form of heat. In others, as in the case of a chemical reaction, the energy that gives rise to this release of heat is derived from some kind of internal potential energy which was previously stored in the arrangements of atoms in the substances involved. An example of an exothermic chemical reaction is when an acid is mixed with a base. In becoming neutralized the chemical potential energies in both reactants are transformed into heat which can be measured by the use of a thermometer which shows a rise in temperature. An example of an exothermic physical process is the condensation of water from a gas to a liquid. Steam (water vapor above 100°C) is dangerous precisely because this process is exothermic. When steam condenses on something it loses energy as heat; this heat raises the temperature of the object upon which the water condensed. Take some advice: never let steam condense directly on your body! In exothermic processes the temperature of the surroundings increases.
When the system absorbs energy from the surroundings the process is called endothermic. Generally, everyday experience provides few examples of endothermic processes and they are therefore a bit harder to understand. Or rather, we generally do not understand the everyday examples to be in fact endothermic. For instance, when water evaporates from a liquid to a gas as in a boiling tea kettle it is an endothermic process. It is not usually identified as such because the temperature of the kettle is so high and we associate high temperatures with exothermic processes. Running electric current through the high-resistance coil of an electric heat element is exothermic. Raising the temperature of water to 100°C and then causing it to evaporate is endothermic: energy must go into the water to make these things happen. Once the water is boiling the heat continues to enter the water but does not raise its temperature. This is because it is used to do the work of breaking the bonds holding the water molecules together. So heat can be added to something and the temperature can stay the same. In endothermic processes the temperature of the surroundings decreases.
Another example of an endothermic process is the formation of a solution of certain inorganic salts. Potassium nitrate (KNO3) has an endothermic heat of solution. This means that heat is absorbed from the surroundings to enable the KNO3 to dissolve. This leads to a reduction in temperature of the water and the vessel in which the solution is made. Heat has been used up and taken away from the water to create the solution.
Find the molar heat of solution for KNO3. First, dissolve 1.00 g of KNO3 in 25.0 g of water at 25.0°C. When this is done in a calorimeter with a specific heat of 48.2 J/°c the final temperature is 22.8°C
qKNO3 + qwater + qcalorimeter = 0345 J 101.1 g 1 kJ -------- * --------- * ------- = 34.9 kJ/mol 1.00 g 1 mol 1000 J
Note that the value for the heat of solution of KNO3 is positive. If you calculated the heat for the calorimeter and water separately they would prove to have negative values. An exothermic process has a negative value for its calculated heat and an endothermic process has a positive value for its calculated heat. This comes about naturally from the basic equation for heat: q = sm(Tf – Ti). When Tf is greater than Ti then temperature increased (ΔT is positive). To raise temperature requires an input of heat. If heat is an input then a process is endothermic. The reverse is true when Ti is greater than Tf.
The following problems will help you to understand the concepts involved in this lab and to be able to do the math required for the analysis of your lab results.
The following list does not cover all possible hazards, just the ones that can be anticipated. Move slowly and carefully in the lab: haste and impatience have caused more than one accident.
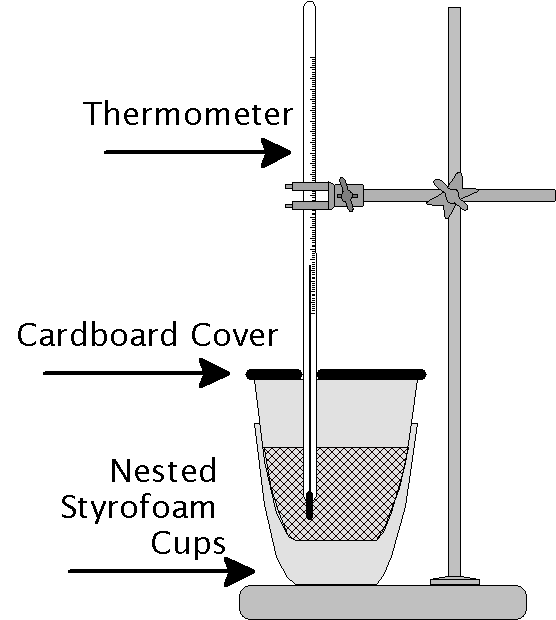
This lab has two main parts. In Part I you will assemble and calibrate your calorimeter. The materials are simple and not at all high-tech and yet will allow you to make very good measurements if you are careful. Using hot water you will find out the heat capacity of the calorimeter. In Part II you will measure the heat of solution of potassium nitrate. Ordinary table salt shows no change in temperature upon dissolving in water. Potassium nitrate on the other hand has a positive heat of solution.
In this part of the lab you will construct a simple constant-pressure calorimeter. Next you will compare two thermometers to ensure that differences in the calibration of the thermometers does not contribute to instrumental error. Next you will mix hot water at a known stable temperature with cold water in your calorimeter. By measuring the final temperature of the mixture you will be able to calculate the heat capacity of your calorimeter.
In this part of the lab you will add a carefully measured mass (~1 g) of potassium nitrate (KNO3) to a calorimeter containing approximately 25 g of water at a known temperature. Because this substance has a positive enthalpy of solution the temperature will drop as heat is removed from the water and calorimeter.
No formal lab report will be required. Answer the following questions in a typed document. For calculations, show only the set-up and result. Do not show all intermediate algebraic steps.
Answer the questions in the analysis section of this lab handout (above) in a typed document.