Hydrogen Atom Simulator

Objective

In this lab students will play with the hydrogen simulator at the Nebraska Astronomy Applet Project (NAAP). The simulator is on the Hydrogen Energy Levels Module page (http://astro.unl.edu/naap/hydrogen/hydrogen.html). While doing so they will learn about the relationships between the wavelength, frequency and energy of photons of light. Also, they will explore how photons interact with the quantum energy levels of the electron in a hydrogen atom.

Overview

In this lab you will review a few facts about the nature of light. First, the wavelength and the frequency of light are related by an inverse proportion: c = λf. (Remember, c = 3.00 × 10⁸ m/s when wavelength, λ, is in meters and frequency, f, is in 1/s, also called Hz). Second, the frequency of light and the energy of a single photon at that frequency are related by a direct proportion: E = hf. (Remember, E is the energy in joules, J, of one photon of light with frequency, f, in Hz; h is Planck’s constant: 6.626 × 10^-34 J· s).

Also in this lab you will explore what the atomic processes of absorption and emission look like. You have been told, but probably do not yet fully believe, that atoms only absorb light in discrete amounts: quantum energies. In this activity you will be able to experience it yourself. In the process you will be able to confirm the visible-light spectrum of hydrogen gas, shown below:

Background

The electron in a hydrogen atom can orbit the nucleus (a single proton) at different distances called Energy Levels. The closer the electron is to the nucleus the lower its potential energy and the farther it is from the nucleus the more potential energy it has. When the electron is as close as quantum physics will allow it to get then it is said to be in the Ground State. The Ground State is called energy level 1. All other orbits around the nucleus are called Excited States. They are numbered up from level 1 in the energy level diagram shown at right.

When an electron moves from a lower energy level to a higher energy level it is called excitation. For this to occur the atom must absorb exactly the right amount of energy: the quantum energy difference between the two energy levels. In this simulation this is only possible when the atom absorbs a photon. Absorption is the process in which an electron in an atom jumps to a higher energy level by using up the energy of a photon. Electrons can be moved to higher levels in other ways (such as by heating up the atoms) but in this simulation absorption is the only possible way.

When an electron moves from a higher energy level to a lower energy level it is called de-excitation. When this happens the electron releases an amount of energy that exactly matches the difference in energies between the two energy levels by emitting a photon. The photon will always have exactly the quantum energy represented by the difference between the energy levels. Emission is the process in which an electron in an atom jumps to a lower energy level by emitting a photon.

Electrons can only occupy certain energy levels with well-defined quantum energies. There is a lowest energy level (the Ground State) and a highest energy level. Beyond the highest energy level an electron becomes free of the atom. When the energy of a photon exceeds a certain amount then no matter what energy the photon has it will cause the electron to fly away from the atom entirely. This event is called Ionization. Ionization occurs when an electron absorbs a photon with more energy than the energy that would take it to the highest available energy level. When an electron joins up with the atom again it is called Recombination.

A note about units. Wavelength must be measured in meters (m) and frequency must be measured in Hz (1/s) to use the c = λf formula. Energy calculated using E = hf is in joules (J). In this simulator wavelength is given in more convenient units: nanometers (nm) and micrometers (µm). One meter equals 1 × 10⁹ nm and 1 × 10⁶ µm (1 m = 1 × 10⁹ nm; 1 m = 1 × 10⁶ µm). Also, it is important to realize that 1 µm = 1,000 nm. Frequency is given in Hz in the simulator but the energy values are given in electron-volts (eV). One eV is equal to 1.602 × 10^-19 J. The eV is a much more convenient unit when you are talking about individual atoms and that is why it is used here. Regardless of the unit, frequency is still directly proportional to energy.

In the visible part of the spectrum (from 400 nm - 700 nm) there are recognizable colors. Light with a wavelength of 400 nm is violet while light with a wavelength of 700 nm is red. You can remember the colors and order of the rainbow using the mnemonic ROYGBIV. You can think of it as a name: Roy G. Biv. The colors, of course, are Red, Orange, Yellow, Green, Blue, Indigo, Violet. They are listed in order of increasing frequency and decreasing wavelength: violet has the shortest visible wavelength and red has the longest.

The very longest wavelengths of IR light cross over into the microwave region of the spectrum. Microwaves have still lower energies and still smaller frequencies.

Light with a frequency higher than that of UV light have shorter and shorter wavelengths. The wavelengths of x-rays are just shorter than UV. Gamma rays have still shorter wavelengths. In order of increasing energy: UV, x-rays, gamma rays.

Questions

1. In the above table compare the photons of light at each end of each row. The first row compares a photon of red light with a photon of blue light. You can see that red light has a longer wavelength, a shorter frequency, a smaller energy and the same speed as a photon of blue light. Circle the appropriate word in each box to compare Photon A with Photon B.

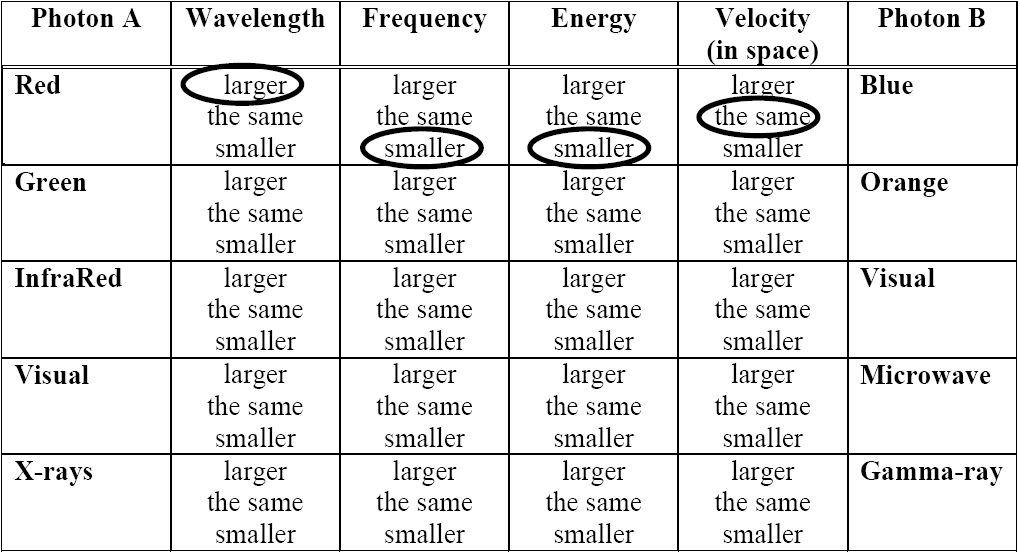
When one variable increases at the same time that another variable increases scientists say that the two variables are directly proportional. A graph of such a pair of variables would be a straight line. When one variable decreases in proportion to the increase of another variable then the relationship is described as inversely proportional. The graph of such a relationship is an inverse curve that looks like y = 1/x.

Use what you already know about light and the results of your work on the table comparing photons to answer the following questions.

2. If you increase the frequency of light what happens to the wavelength?
3. Is the relationship between wavelength and frequency a direct proportion or an inverse proportion? Give an example to support your answer.
4. If you increase the frequency of light what happens to the energy?
5. Is the relationship between energy and frequency a direct proportion or an inverse proportion? Give an example to support your answer.

Using the Simulator

For each energy level of an atom there are three energy ranges for photons that interact with the atom.

• Range 1: No photons below a certain energy can affect the electron in its current energy level at all.
• Range 2: In this range some photons cause the electron to jump to a higher level and some don’t; it depends on the precise value of the energy of the photon.
• Range 3: Above a certain energy all photons cause the electron in its current energy level to be ionized; the energy is so high it causes the electron to fly away from the nucleus.

6. Ground State, Level 1
   1. Range 1: Is there any effect on the e^- in the ground state when you fire a photon with an energy less than 10.2 eV? Why or why not?
   2. Give the frequency (f), wavelength (λ), and energy per photon (E) of three photons (one IR, one visible, and one UV) with an energy less than 10.2 eV. Select them at random using the slider in the simulator. Fire each photon and record the results below.
   Range 2: Fill in the following table by finding the wavelength, frequency, and energy for each of the transitions shown. Also, record the spectrum region.

   Wavelength	Frequency	Energy	Transition	Region
   122 nm	2.5 × 1015 Hz	10.2 eV	1 --> 2	UV
   			1 --> 3
   			1 --> 4
   			1 --> 5
   			1 --> 6

   Hint: There are some buttons labelled L_α, L_β, L_γ, L_δ, and L_ε. These are helpful for filling in this table.
   Range 3: Identify the smallest energy (smallest frequency, longest wavelength) that you can fire at the atom and cause the electron to be ionized. Hint: look at the value of the potential energy of the electron when it is in Level 1.
   f =                           λ =                           E =                           Spectrum Region: IR   Vis   UV

7. First Excited State, Level 2
   Drag the electron from the ground state to level 2 to answer all questions in this section.
   1. Range 1: Is there any effect on the e^- in the ground state when you fire a photon with an energy less than 1.9 eV? Why or why not?
   2. Give the frequency (f), wavelength (λ), and energy per photon (E) of two photons (one IR and one visible) with an energy less than 1.9 eV. Select them at random using the slider in the simulator. Fire each photon and record the results below.
   Range 2: Fill in the following table by finding the wavelength, frequency, and energy for each of the transitions shown. Also, record the spectrum region.

   Wavelength	Frequency	Energy	Transition	Region
   			2 --> 3
   			2 --> 4
   			2 --> 5
   			2 --> 6

   Hint: There are some buttons labeled H_α, H_β, H_γ and H_δ. These are helpful for filling in this table.
   Range 3: Identify the smallest energy (smallest frequency, longest wavelength) that you can fire at the atom and cause the electron to be ionized. Hint: look at the value of the potential energy of the electron when it is in Level 2.
   f =                           λ =                           E =                           Spectrum Region: IR   Vis   UV
8. With the electron in the Ground State try hitting the L_α twice in a row without allowing the electron to undergo de-excitation back to the Ground State. What happens? Why?
9. Drag the electron to the 1^st Excited State (Level 2). Hit the H_β button twice. What happens? Why?
10. What condition has to be met in order for an electron to jump from one energy level to another?
11. Under what conditions will an electron become ionized when it absorbs a photon?
12. What happens to an electron in an excited state if left alone long enough? Why? What is this process called?
13. Which series of buttons under the sliders belongs to the spectrum of hydrogen gas on the first page of this packet? Which energy level is an electron returning to when light of these wavelengths is emitted?