Your Name:
Date:
Class:

Measurement and
Significant Figures

Accuracy is about whether a measurement agrees with the true value. If a measurement is accurate then it is correct. This can be difficult to determine unless it is possible to look up a result in a trusted source.

Precision is about whether several measurements of something agree with each other. Precision can be measured using the range of values. One half of this range is the amount by which the true value may vary above and below the average value (this is called the plus-or-minus amount—the ± amount). In lab activities we make several measurements in order to be able to calculate just how precise you are. Chances are good, but not certain, that if your measurements have a small range then your results are accurate, too. One thing is sure, though: the smaller the plus-or-minus amount, the more precise the measurement is.

See also this handout about Accuracy and Precision.

The precision of a result is reflected in the number of digits reported. If you have a bathroom scale and measure the mass of a book with it you might find it weighs 7 pounds. A more precise scale might reveal that the weight of the book is actually 7.15 pounds. This second number is more precise. When a measurement is expressed with more digits it is more precise than a measurement of the same thing showing fewer digits. The significant figures of a measurement are all the digits known for sure plus one estimated digit.

Errors in the lab come in three types. First, human error. Human error is when you make a boneheaded mistake. For example, say you intend to measure out 1.0 g of a chemical but instead measure out 10.0 g. This type of mistake can be avoided and will be noticed while you are working if you are paying attention. Second, there is systematic error. Systematic error leads to measurements being always high or always low. The change is in the same direction for each measurement and is always the same size. This type of error occurs, for example, if you use a ruler to make measurements by pushing the end of the ruler up against something. Many rulers do not have their zero mark right at the end. This results in all your measurements being too long by the extra bit of ruler. Third, there is random error. Random error is the variation in a measurement up and down around the true value of a quantity. Random error can be seen in a set of data that represent measurements of the same quantity. The quantity is a constant and has some true value but the measurements of it are usually a bit too high or a bit too low. For each individual measurement the amount that the measurement is too high or low is random. It can be safely assumed that random error will affect every set of measurements that anyone makes. It occurs because we estimate the last digit of a measurement and different people estimate that last digit differently. Random error may also occur because the value displayed by an electronic instrument may fluctuate and it is up to the observer to make a judgment about the value. Random error can be measured by using the range of measurements to calculate a plus-or-minus amount. The plus-or-minus amount is one-half of the range. It can also be measured using the percent random error. This is calculated by dividing the plus-of-minus amount by the average and multiplying by 100%.

Unless otherwise noted the final significant figure (the last digit) in a measurement is assumed to be ±1. So 9.45 kg is 9.45 ± 0.01 kg—that is, the true value is assumed to be between 9.44 kg and 9.46 kg. Random error’s influence over results can be reduced by taking multiple measurements of the same thing and averaging the results. This evens out the too-high measurements with the too-low measurements.

Estimating the Last Digit

The maximum possible precision is defined as one tenth (1/10 or 0.1 times) the smallest division on the measuring instrument. On the first ruler shown below there are marks only every centimeter. So the best precision comes by estimating the last digit which is 0.1 × 1 cm = 0.1 cm. The maximum possible precision can be expressed as a plus-or-minus amount and is ±0.1 cm. For the second ruler the plus-or-minus amount is 0.1 × 0.1 cm = 0.01 cm. This ruler is ten times more precise than the one above it at ±0.01 cm.

Look at the rulers below and use each one in turn to measure the gray line. Remember, precision is limited to one tenth of the smallest division. For each ruler estimate the last digit. That is, for the first ruler, estimate to the tenths place. For the second ruler estimate to the hundredths place.

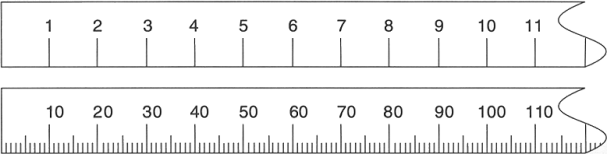
To do the estimating you must imagine that the space between the markings on the ruler can be divided into ten smaller spaces. Use these imaginary spaces to measure the last digit.

Here is a key point: When you estimate the last digit you are actually making your measurement more precise. First, you have added a significant figure: more significant figures means better precision. Second, you are making the digit before the last digit more secure due to the fact that you are observing the last digit so closely.

Procedure

Part I

For the following measurements and calculations pay close attention to the number of significant figures and use the rules for doing calculations with significant figures.

1. As an individual please use a ruler or meter stick to measure the following items:
   the length of a paperclip
   the length, width, and height of a book (everyone in a group will use the same book)
   
2. Compute the volume of the book
3. With at least four other students put all of your results into one neat table; make sure everyone makes his/her own table
4. For your group’s data compute an Average for each of the things you had to compute above
5. For each measurement compute the Range: take the largest value and subtract the smallest value from it
6. For each measurement express the range as an amount above or below the average: divide the range by two—this is your ± Amount (Plus-or-minus Amount)
7. Report Results in this way: 4.2 ± 0.2 cm. Round the plus-or-minus amount to one digit. Round the last digit of the average to match the place value of the remaining digit in the plus-or-minus amount. This is how you use your data to decide the appropriate number of significant figures.
8. Compute the Percent Error for each result (divide the plus-or-minus amount by the average and multiply by 100%). This value tells how big the random error is relative to the size of the measurement.

Use the following data table to collect your data. If you find that the boxes are too small then make the data table in your lab notebook. Remember, every individual student must have their own copy of these data so everyone must write it down. The numbers 1 - 4 in this data table represent different individuals making measurements of exactly the same object.

Here are some sample data I collected for the paperclip in cm: 3.30, 3.28, 3.29, 3.30. Average: 3.29 cm, Range: 0.02 cm, ± Amount: 0.01 cm, Result: 3.29 ± 0.01 cm, Percent Error: 0.30%.

	Paperclip	Book
	Length (cm)	Length (cm)	Width (cm)	Height (cm)	Volume (cm3)
1
2
3
4
Average
Range
± Amount
Result
Percent Error

Check-in ______

When you have completed your work in this section check in with your teacher. Initials will be given for a complete set of data and calculations.

Part II

You will select three objects to weigh: one large, one medium, and one small.

1. Have each member of the group measure the mass of three items of your choice. Each and every person must make their own measurements independently of the others. Reset the balance between measurements.
2. Construct a table of the group’s data and find the average, range, plus-or-minus amount, result and percent error for each item; every member of the group must do this

Check-in ______

Part III

There are several graduated cylinders at the back of the room. These instruments are used to measure the volume of liquids. Each one has a limit to its precision. See if you can find out whether there is a relationship between the size of a graduated cylinder and its precision.

1. Determine the maximum precision of each graduated cylinder, expressed in mL. Do this by writing down the digit or decimal point that is estimated for each one.
2. Have each member of the group carefully read the volume in each of the graduated cylinders
3. Construct a table of the group’s data and find the average, range, plus-or-minus amount, result and percent error for each cylinder; every member of the group must do this

Check-in ______

Grading

For this lab you must turn in your lab handout with all check-ins, the completed data tables and answer the lab questions at the end of this handout. In a typed document answer the questions below on a separate piece of paper. All numbers must be expressed with the correct number of significant figures.

You will be graded on the quality of your writing, the professionalism of your work’s appearance, and the quality of the answers to the questions.

Questions

1. The precision of an instrument is limited by how close together the lines are on that instrument. The maximum precision is the decimal digit that is estimated when you use the instrument. What is the precision of the metersticks or rulers you used in class based on the marks on the ruler? In other words, what is the last decimal digit that can be estimated using the lines marked on it? Report your answer in centimeters and explain why it is what it is.
2. Consider the plus-or-minus amounts you calculated for your length measurements. If you are using the meterstick correctly to make valid measurements then the only estimated digit should be in the hundredths place. Therefore, if you are using the meterstick correctly your plus-or-minus amounts should all be between ±0.01 and ±0.09. Are your plus-or-minus amounts in this range? Why or why not?
3. Compare the plus-or-minus amounts for your volume calculation with the plus-or-minus amounts of your length measurements. Which is more precise? How does combining measurements in a calculation affect precision?
4. Which of the graduated cylinders could distinguish the smallest differences between two measurements? In other words, which one had its estimated digit furthest past the decimal for measurements of milliliters?
5. Which of the graduated cylinders had the largest value for the certain digits and the estimated digit?
6. Is it theoretically possible to make a valid measurement—with only one estimated digit—which could distinguish between a volume of 55.42 mL and 55.43 mL? Why or why not?
7. What digits are certain and which digit is estimated when using the three-beam-balance?
8. Even if all the members of your group used the balance exactly correctly you would not all agree about all the digits of a measurement. Explain why not. Also, what digit or digits would you expect would be the only one(s) to vary if everyone uses the balance correctly?
9. If you look at the data collected by your group do your measurements agree for all of the certain digits? Since the variation in measurements ought to only be in the uncertain digit what should you do if you had a larger amount of variation?
10. How many certain and how many estimated digits should be in every valid measurement?
11. Which measurement has higher precision: 4 cm or 4.05 cm? Explain how you know. Draw a ruler that could be used to make each of these measurements in a valid way. What makes the rulers different from one another?
12. Consider the following set of data:
    456.324 cm², 455.995 cm², 456.198 cm², 455.884 cm²
    Calculate the average, range, plus-or-minus amount, and percent error. Report the result showing the correct number of significant figures with the ± amount.
13. What do you use to find out the amount of variation in your measurements? How can the plus-or-minus amount be used to round off your average to the correct number of significant figures?
14. What is human error? Give three examples.
15. What is systematic error? Give two examples.
16. What is random error? Describe a method you can use to measure the amount of random error in your data collection.
17. The percent error in a measurement is calculated by dividing the plus-or-minus amount by the average measurement and multiplying by 100%. You have already calculated the percent error for all of the measurements in this lab. For each one evaluate whether you had excellent, good or poor precision. Excellent precision is 1% or less. Good precision is between 1% and 3%. Poor precision is when the result is greater than 3%. Choose one measurement and explain how you managed to have excellent precision. Choose another and explain why the precision was poor.