This lab is a computer-simulation-based activity. The simulator is available for immediate use in any browser at https://phet.colorado.edu/sims/html/isotopes-and-atomic-mass/latest/isotopes-and-atomic-mass_en.html. Or, perhaps more easily accessed by performing a search for “PhET Isotopes and Atomic Mass”.
Atoms of an element come in varieties called isotopes. Isotopes are atoms of the same element which have different mass numbers. Remember, the mass number of a specific atom is the sum of the protons and neutrons in its nucleus. In order to be atoms of the same element, isotopes must have the same number of protons. They have different mass number due to their having different numbers of neutrons.
Some isotopes of an element are stable, that is, they are not radioactive. Others may exist in nature or only in the lab when they are made artificially. Still others are simply impossible to make. For example, helium has two naturally occurring isotopes, helium-3 (32He ), and helium-4 (42He ). Both of these are stable but one of them is a lot easier to find in the environment than the other. Only one out of a million helium atoms is a helium-3 atom. There are absolutely no helium-2 atoms in the world and none can ever be made. A helium-2 atom would have two protons but zero neutrons and with no neutrons an atomic nucleus can’t remain whole.
The naturally occurring isotopes of an element each have a natural abundance. The natural abundance of an isotope is the percentage of all atoms of that element which have the mass number of that isotope. For example, 80.1% of all boron atoms in nature have the mass number 11. So we say boron-11 (115B) has an abundance of 80.1%. The only other naturally occurring isotope of boron is boron-10 (105B), which has an abundance of 19.9%. How can we understand the idea of abundance? Imagine we have 1,000 atoms of boron. On average, 801 of them will be boron-11 and 199 of them will be boron-10.
Isotopes are identified by their mass numbers. Natural abundances are measured by scientists using an instrument called a mass spectrometer. The same instrument can be used to measure the third important characteristic of isotopes which is their atomic mass. The atomic mass of an isotope is the actual mass of that isotope in amu. For example, boron-10 atoms have an atomic mass of 10.01294 amu and boron-11 atoms have a mass of 11.00931 amu.
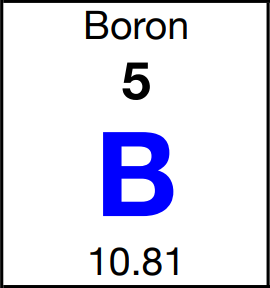
Chemists need to know the mass of atoms because we use that information to be able to count atoms by weighing them. That’s what the atomic mass that’s shown on the periodic table is for. If we take a look at the box for boron on the periodic table we can see that the atomic mass of boron is 10.81 amu. This is neither 10.01294 amu nor is it 11.00931 amu. All atoms of boron have either a mass of 10.01294 amu or 11.00931 amu and no atoms of boron have a mass of 10.81 amu. So what does the 10.81 amu represent? It is the average atomic mass of boron. The average atomic mass of an element is the average mass of its isotopes. This average must take the natural abundances of the isotopes into account. To find the average it is not enough to add up the isotopes’ masses and divide by the number of isotopes. For boron, this would give:
(10.01294 amu) + (11.00931 amu)
------------------------------- = 10.51 amu
2
The figure 10.51 amu is wrong. The correct average mass must account for the fact that 801 out of 1,000 boron atoms have a mass of 11.00931 amu and 199 out of 1,000 have a mass of 10.01294 amu. Here is how that calculation works:
(0.199)x(10.01294 amu) + (0.801)x(11.00931 amu) = 10.81 amu
You convert each percentage for the natural abundance to a decimal, multiply each one by its matching isotope mass, and add them together. Another way to do it is to imagine you have 1,000 atoms of boron. In that case you multiply each isotope mass by the number of atoms of that isotope, add it all together and divide by 1,000:
(199)x(10.01294 amu) + (801)x(11.00931 amu)
-------------------------------------------- = 10.81 amu
1,000
Because the natural abundance of an isotope is included in the calculation of the average atomic mass of all of the atoms of an element it has an effect on that average. The average atomic mass will be closest to the isotope with the larger natural abundance. For example, the average atomic mass of boron is closer to the atomic mass of boron-11 than it is to atomic mass of boron-10. This makes sense because boron-11 makes up 80.1% of all boron atoms.
When you open the simulator you will be on the Home tab. Click on the Isotopes tab at the bottom of the screen. When you get to that tab, click the buttons that will make the “Symbol” and “Abundance in Nature” displays open up.
Fill in the following table by creating all of the stable isotopes of each element in the table below with the simulator and recording what you see on your screen. To switch elements you use the segment of the periodic table in the upper-right part of the screen. You will have to switch back and forth between “Mass Number” and “Atomic Mass (amu)” on the display under the atomic model. If you are doing this on a piece of paper, please take care to set up a neat table like the one you see on your screen.
| Isotope Name |
Complete Isotope Symbol |
Number of
Protons |
Number of
Neutrons |
Mass Number |
Atomic Mass (amu) |
Abundance in Nature |
| Hydrogen | ||||||
| Hydrogen | ||||||
| Boron | ||||||
| Boron | ||||||
| Carbon | ||||||
| Carbon | ||||||
| Fluorine | ||||||
| Neon | ||||||
| Neon | ||||||
| Neon |
Next, click on the Mixtures tab at the bottom of the simulation screen. On that screen select Hydrogen (H) from the periodic table and open the “Percent Composition” and the “Average Atomic Mass” displays. At bottom-right click the button that says “My Mix”. Just under the main display, which is currently a black rectangle, there is a button with an icon that looks like a bucket and another that looks like a slider. Click on the slider button.
[(Mass of Hydrogen-1) + (Mass of Hydrogen-2)]
------------------------------------------------ =
2
(Mass of Hydrogen-1) × 50 + (Mass of Hydrogen-2) × 50
-------------------------------------------------------- =
100
(Mass of Hydrogen-1) × 10 + (Mass of Hydrogen-2) × 90
-------------------------------------------------------- =
100
(Mass of Hydrogen-1) × (0.10) + (Mass of Hydrogen-2) × (0.90) =
(Mass of Hydrogen-1) × (0.999885) + (Mass of Hydrogen-2) × (0.000115) =
(Mass of (Percent (Mass of (Percent Isotope × Composition + Isotope × Composition + … = Average Atomic Mass One) One) Two) Two) If you have more than two isotopes, you just insert the mass and percent composition of each additional isotope.