Carbon monoxide binds to the oxygen-carrying protein hemoglobin in the blood 200 times more strongly than oxygen. When present, it prevents oxygen from binding to hemoglobin and this prevents it from reaching the body’s tissues. At a level of just 100 parts per million by volume in air it can cause dizziness and headaches. When its concentration reaches 667 ppm it can be fatal. The moral of the story: never run a generator (or burn charcoal) in an unventilated room.

Incidentally, take notice of the fact that both equations for the burning of pure carbon are what are called balanced chemical equations. That is, there is one atom of carbon and there are two atoms of oxygen on both sides of the equation showing the product CO₂. In the equation showing the product CO it takes two atoms of carbon to react with one molecule of oxygen: as a result two molecules of CO are formed.

Conservation of Mass

Carbon monoxide results from burning fuel without enough oxygen. So how much oxygen do you need to make sure that all the carbon burns to form CO₂ and not to form CO? This is a question chemistry can help us to answer. We know that in a balanced chemical equation the number of atoms that react are the same as the number of atoms after the reaction is over.

C + O₂ CO₂
(reactants—one carbon atom and two oxygen atoms— react to make
products—a compound made of one carbon atom and two oxygen atoms)

The ratio  ⁸/₃ is a ratio of masses. That means that for any size mass of carbon you can figure out how much oxygen you need (by mass, if not by number of molecules). So say you have exactly 12 g of carbon (grams can be measured using a simple lab balance; atomic mass units are not so easy to measure). That means that you need 32 g of oxygen to react with it to make carbon dioxide: 12 g ×  ⁸/₃ = 32 g. By putting oxygen into a container of known mass sitting on a balance you can measure out 32 g of the gas. If you ignite the 12 g of carbon inside the container holding 32 g of oxygen they will both be used up and the container will then be filled with carbon dioxide.

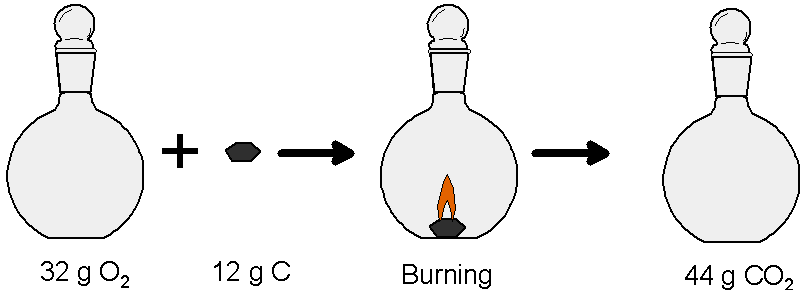
Take notice of what just happened here. The ratio of masses depends on the idea that an individual carbon reacts with exactly one oxygen molecule. That is, because you know how many atoms of each element react you also know what mass of each element reacts. By using the ratio of the masses you can figure out what measurable mass, in grams, of each element will be needed for the reaction. So by weighing out twelve grams of carbon and 32 grams of oxygen you have in effect guaranteed that there are the same number of carbon atoms in twelve grams of carbon as there are oxygen molecules in 32 grams of oxygen.

This result is very important. Atoms and molecules are unimaginably small: a CO₂ molecule is about 0.29 nm long. That is 0.29 billionths of a meter long or 0.29 millionths of a millimeter. Written in decimal notation the length of the molecule is 0.000 000 000 29 m.

Their masses are also incredibly tiny: a single molecule of O₂ has a mass of 5.3 × 10^-23 g. No lab balance ever made could possibly measure such a tiny mass. Another reason being able to count molecules and atoms by weighing them is important is that there are so incredibly many of them. The amount of air you breathe in for each breath is about 0.5 L. This is actually a staggeringly large number of gas molecules: about 1.2 × 10²². The discussion above shows how it is possible to figure out relative numbers of atoms based on nothing more than the mass of the substances.

The Mole

Chemists have to deal with astonishingly small sizes and inconceivably large numbers if they want to understand what is going on in chemical reactions and physical changes. They do it by the simple method of weighing in order to count things. If you go to the hardware store to buy nails there is a good chance that they will weigh your purchase and not count each individual nail. If you have a stack of paper and you want to know how many sheets you have the simplest way to find out is to weigh the stack and divide by the weight of one sheet.

In the same way chemists use the mass of a pile of atoms or molecules to figure out how many atoms or molecules are there. They take one more step to simplify things even further. Chemists use a unit called the mole to keep track of the number of atoms or molecules. The mole is a unit like the dozen, the pair, the six-pack or the ream (a ream of paper is 500 sheets). There are twelve things in a dozen, two in a pair, six in a six-pack and 500 in a ream.

How many things are there in a mole? There are as many things in a mole as there are carbon-12 atoms in exactly 12 g of pure carbon-12. This definition alone would be enough for the mole to be a useful unit since carbon can be reacted with other elements and compounds, the results analyzed and in this way the mass of a mole of other chemicals can be determined. Even so, it is interesting to see just how big of a number the mole is. If it were possible to have a mole of chicken eggs they would cover the entire surface area of the Earth…four miles deep. If you were rich enough to own a mole of pennies then they could be stacked in groups 400 pennies high in a disk that reaches from the surface of the Earth all the way to the orbit of the moon. (The bank teller would hate you for bringing them in for a deposit; it is enough money so that if distributed evenly every person on Earth would have over 1 trillion dollars.) One more illustration: the volume of the Earth is about 10²¹ m³. It takes about 500 grapefruit to fill up a box one meter on a side (1 m³). So a mole of grapefruit would be large enough to fill the entire volume of the planet Earth.

Enough illustrations: a mole is a quantity of 6.02 × 10²³ items. In theory, you could have a mole of any kind of thing. A mole of water molecules has the same number of items as a mole of elephants. The elephants take up a lot more space, however. But the point is not really how many items there are in a mole. The point is what the mole can do. We saw earlier that 12 g of carbon and 32 g of oxygen have the same number of particles. Now you should be able to figure out that that number of particles is a mole.

For any singular atom or molecule it is easy to figure out the mass measured in atomic mass units (amu). The mass of a CO₂ molecule is 12 amu + 2 × 16 amu = 44 amu. The mass of an O₂ molecule is 2 × 16 amu = 32 amu. The mass of a single unit of NaCl is 23 amu + 35 amu = 58 amu. The great thing about the mole is that there are a mole of atoms or molecules in the mass of a substance in grams that is equal to the mass of a single unit of that substance in atomic mass units. In other words, there is a mole of CO₂ molecules in 44 g of CO₂. Likewise, 32 g of O₂ is a collection of a mole of oxygen molecules. Similarly, if you measure out 58 g of NaCl you have, at the same time, counted out a mole of NaCl units.

For many people this is a difficult concept. Perhaps this illustration might help. Say you have a dozen crocodiles and a dozen mice. There are twelve of each animal but you could never say that the two groups of animals have the same mass. It would only take one crocodile one snap of its jaws to consume the dozen mice! On the other hand, if you have 1,000 kg of crocodiles and 1,000 kg of mice you would have the same mass of each one. But you would certainly not have the same number of each animal. How many mice (weighing in at 25 g) would that be? A single average adult crocodile might have a mass of 1,000 kg.

Questions and Problems

Comprehension Questions

Answer the following questions using one or more complete sentences. Everyone in the group must write down complete answers. Discuss among your group members what the best way to answer the question is and then write it down. All members must write down the answer or risk losing participation points.

1. Definitions Write definitions in your own words using what you have learned about the concepts listed. Do not copy a definition from somewhere else!
   1. chemical reaction:
   2. physical change:
   3. balanced chemical equation:
   4. mole:
   5. mass:
   6. quantity:
2. Please explain, in a short paragraph, what the conservation of atoms has to do with the principle of the conservation of mass in chemical reactions and physical changes.
3. Please explain, using chemical equations, why it is a very bad idea to run a gasoline engine indoors.
4. For the equation describing the burning of carbon to make carbon monoxide what is the ratio of the mass of carbon burned to the mass of oxygen used? How much oxygen (in grams) would be needed to burn all of a sample of 24 g of carbon to make carbon monoxide?

Comprehension Questions, continued

5. Recall from the text the argument which relates the number of atoms to the mass of reactants and products in a chemical reaction. Relate this argument in your own words and show how it is possible to use a balanced chemical equation to find the mass of each chemical which has the same number of particles. Discuss the reasons why being able to do this are important.
6. Invent a new unit of quantity called the strand. It is used to count grains of sand. Describe how you would go about defining the unit and establishing a method for counting grains of sand. Carry out your method using whatever lab equipment seems appropriate. Report your results here.
7. You have been given some number of textbooks with a total mass of 1,400 kg. Each text has a mass of 1.5 kg. You have also been given 900 spiral-bound notebooks, each with a mass of 300 g. Do you have more textbooks or more notebooks? Also, do you have a larger mass of textbooks or notebooks?
8. Mr. Keller is 180 cm tall. Imagine you had a mole of Mr. Kellers. If all of them were to lie on the ground end to end how long would the line be? Convert your answer to km (100,000 cm = 1 km). Would the line reach to the Moon’s orbit at 1.74 × 10³ km? Would the line reach the Sun, which is 1.5 × 10⁸ km away? How many times would the line go around the Earth, with a circumference of 4.0 × 10⁴ km?
9. A chemistry teacher would like to order a mole of sand grains in order to show his students just how big a mole really is. One grain of sand has a volume of about 4 × 10^-9 m³ if it has a radius of 1 mm. Dump trucks with a volume capacity of 11 m³ are going to be used to transport the sand to the school. How many dump truck loads will be needed?

Chemical Equations

Chemical equations express possibly the most important chemical law ever discovered. Antoine Lavosier, considered by many to be the father of modern chemistry, expressed this law as follows:

“We may lay it down as an incontestible axiom, that, in all the operations of art and nature, nothing is created; an equal quantity of matter exists both before and after the experiment; the quality and quantity of the elements remain precisely the same; and nothing takes place beyond changes and modifications in the combination of these elements.”

That is, matter is neither created nor destroyed. The amount and type of chemical elements remain the same before and after a chemical reaction; they are simply rearranged into different chemical compounds.

Chemical compounds are combinations of elements which cannot be separated by physical means (by freezing, boiling, or sorting). They exist as a result of chemical bonds between atoms of different elements. A chemical compound is defined by the ratio of each type of atom involved in the compound. Here are some examples:

AlCl₃ is a compound of aluminum and chlorine. In each molecule of this compound there is always just one Al atom and exactly 3 Cl atoms.

K₂SO₄: two atoms of potassium, one atom of sulfur and four atoms of oxygen

Fe(OH)₃: one atom of iron, three atoms of oxygen, and three atoms of hydrogen.

The little numbers below and to the right of the atomic symbols (K) and groups of atoms (OH) in these compounds are called subscripts. The subscripts tell you how many of each kind of atom are in the compound. When balancing chemical equations you may never change the subscripts. Changing subscripts changes the compound. For example, H₂O is harmless but H₂O₂ is a strong oxidizer and is used as bleach and to kill bacteria.

In chemical reactions, which are represented by chemical equations, it is often the case that more than one molecule of a compound is required to react with the others. This is shown by a coefficient as follows:

2H₂: there are 2 x 2 atoms of hydrogen (a total of 4).

2H₂O: there are 2 x 2 atoms of hydrogen (a total of 4) and 2 x 1 atoms of oxygen (a total of 2).

2(NH₄)₂S: there are 2 x 1 x 2 atoms of nitrogen (a total of 4), there are 2 x 4 x 2 atoms of hydrogen (a total of 16), and 2 x 1 atoms of sulfur (a total of 2).

Coefficients in front of chemical formulas are multipliers. A coefficient of 2 means that every atom is multiplied by two. If an atom or group of atoms has a subscript, then the subscript is multiplied by two as well.

Each of the following problems gives a chemical formula either with or without a coefficient. Write the number of each type of atom in a chart.

How to Balance a Chemical Equation

Now that we have the background necessary, let’s move on to balancing chemical equations. The following is one method for taking on this challenging task.

1. Count the atoms of each kind on the reactant (left) side and product (right) side.
2. Find the least common multiple (LCM) for each type of atom.
   

   For example, in the unbalanced equation O₂ --> O₃ the LCM is six. That means that there should be 6 oxygen atoms on each side of the equation. The equation is balanced by changing coefficients until this is so:
   3O₂ --> 2O₃

3. Sometimes, adding a coefficient to one formula to balance one kind of atom will throw the other atoms out of balance. Just keep track and go back to fix it.

   For example, in the unbalanced equation KClO₃ --> KCl + O₂ the K and Cl are balanced with one of each on both sides of the equation. The oxygen has an LCM of 6 so you add coefficients: 2KClO₃ --> KCl + 3O₂. This makes it so that K and Cl don’t balance anymore. But by noticing that the LCM for both elements is now 2 you can add a coefficient to KCl on the products side to get the equation to balance: 2KClO₃ --> 2KCl + 3O₂

   The key here is to make a series of changes, each of which gets you closer to a balanced chemical equation.
4. Sometimes atoms of one element appear more than once on one side of an equation. Balance those last. Find the elements which appear in the fewest numbers of molecules and balance them first. Continue in sequence until you balance the element which appears in the most molecules last.
5. Since hydrogen is likely to appear in many molecules in an equation, save balancing it until you have balanced other elements first.
6. Balance molecules of O₂ or molecules that contain oxygen after you have balanced hydrogen.
7. Never change subscripts: don’t be tempted to change NaCl to Na₂Cl since that does not exist. Do not change H₂O to H₂O₂ since they are not the same chemical.
8. Do not put a coefficient in the middle of a formula. It just doesn’t work! (Do not write something like H₂2O).
9. A chemical equation is properly balanced only when the final set of coefficients are all whole numbers with no common factors other than one. For example, this equation is balanced:
   4H₂ + 2O₂ ---> 4H₂O
   but all the coefficients have a common factor of two. The best way to write this equation is:
   2H₂ + O₂ ---> 2H₂O

Some Examples

Here is an example of how to approach the problem of balancing a chemical equation: Fe + O₂ ---> Fe₂O₃
In the unbalanced equation, there is only one Fe on the left and two on the right. Putting a two in front of the Fe on the left brings the irons into balance.
2Fe + O₂ ---> Fe₂O₃
Now the oxygen needs to be balanced. This is a common problem, here is how to solve it:

1. The oxygen on the left comes in units of two, the oxygen on the right in units of three. The LCM is 6
2. Put a coefficient of 3 in front of the oxygen on the reactant side. Put a coefficient of 2 in front of the Fe₂O₃ on the product side.

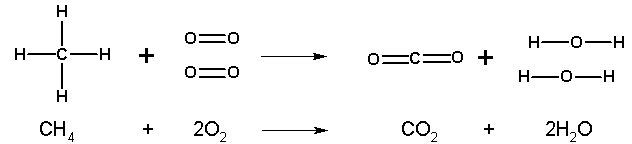
Methane is the largest component of natural gas, which is used in bunsen burners. All combustion reactions involve the combination of the fuel with oxygen to produce carbon dioxide and water.

CH₄ + O₂ --> CO₂ + H₂O

Balancing Chemical Equations

Balance the following chemical equations. Please write neatly and clearly indicate the final answer for each problem. Show your work.

Moles: Quantities and Masses

Molar Masses

For each of the following elements or compounds calculate the mass of 1 mole of particles of that substance. Express answers in units of g/mol.

            60 g                              1 mol
2.4 mol × -------- = 144 g           12 g × -------- = 0.20 mol
            1 mol                             60 g

In the following problems, find the number of moles given the number of grams. Find the number of grams given the number of moles.

Comparing Quantities

Write an equal sign (=), a greater than sign (>), or a less-than sign (<) between each of the following pairs. Determine which sign is appropriate by comparing the quantity of each member of the pair. That is, compare the number of atoms or molecules in each member of the pair. For example, there are more atoms in 28 g of N₂ than in 2 g of C. This is because 1 mole of N₂ has a mass of 28 g. One mole of C has a mass of 12 g. Since there are only 2 g of C and this is equal to 0.17 mol there are more molecules of N₂ in 28 g of N₂ than in 2 g of C.

Comparing Quantities, continued

Big Numbers

For each of the following calculate the number of units of a chemical substance (atoms or molecules or ionic unit). For example, 1.5 mol of sugar molecules contains 1.5 × (6.02 × 10²³) = 9.03 × 10²³ sugar molecules.

Chemical Ratios (Stoichiometry)

The word Stoichiometry (stoy'-ki-AH-me-tree) comes from the Greek stoicheion, which means to measure the elements. It is a technique for finding out how much of a chemical product you will get from a chemical reaction. It can also be used to figure out how much of a starting material you need to get a certain amount of a chemical product. It is arguably one of the most important pieces of chemical knowledge.

It works like this. A balanced chemical reaction is used to figure out the mathematical relationships among the reactants and products. These relationships take the form of ratios. Take an equation used in the text at the beginning of this group activity: 2C + O₂ 2CO. This equation shows that there is a 2:1 molar ratio between C and O₂. That is, it takes one mole of O₂ to completely burn up two moles of C. This is a direct logical conclusion from the idea that it takes one whole molecule of O₂ to react with two atoms of C. Similarly, there is a 1:1 molar ratio between C and CO and a 1:2 molar ratio between O₂ and CO.

Answer the following questions using equations you balanced earlier in this activity. Use a separate sheet of paper to work out the solutions, showing all work. One is done as an example.