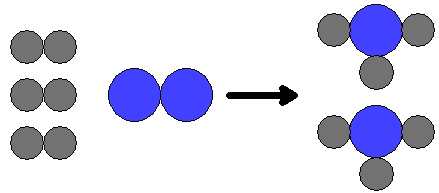
3H2 + N2
 |
| The image above depicts this reaction: 3H2 + N2 |
Your teacher needs to make cookies for a bake sale and so has decided to quadruple the recipe. Supplies are low, however, and even though there is plenty of flour and white sugar, etc., there is only enough brown sugar to triple the recipe. So the recipe is tripled, not quadrupled. The amount of cookies made depends on the ingredient that is in shortest supply. When the brown sugar is used up, no more cookies can be made.
Here is an example of the same idea in a chemical reaction. Nitrogen can be reacted with hydrogen to make ammonia:
At the molecular level this reaction can be illustrated as seen at right. If you double the number of nitrogen molecules, then you have to double the number of hydrogen molecules in order to react all of the nitrogen. This is because of the stoichiometric calculation:
3 H2
2 N2 × -------- = 6 H2
1 N2
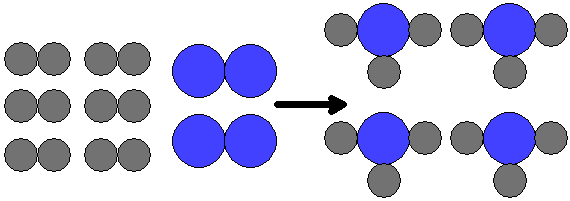
|
| The image above depicts this reaction: 6H2 + 2N2 |
An illustration of this situation is shown at right. Notice that when nitrogen molecules are doubled, so is the number of ammonia molecules. But what if when the number of nitrogen molecules is doubled the number of hydrogen molecules is not doubled? Say there are 2 N2 molecules but only 3 H2 molecules. What happens then? The answer is that there is too much nitrogen for the amount of hydrogen. One molecule of N2 will react but one will be left over because there are no more H2 molecules to react with it. This situation, and its results, are shown below.
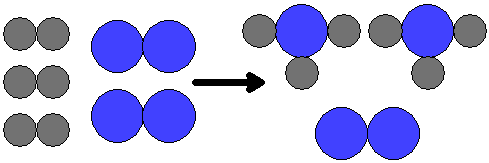
|
| This illustration shows what happens when 3 molecules of hydrogen are reacted with 2 molecules of nitrogen. Two molecules of ammonia form and one molecule of nitrogen is left over. |
The scenarios described above introduce and illustrate the concept of the limiting reactant. A limiting reactant is the chemical for which the supply is less than the molar ratio required in the balanced chemical equation. Consider the combustion of propane:
If a problem states that one reactant is ‘unlimited’ it means that the other reactant is the limiting reactant. Take the case of unlimited oxygen: how much carbon dioxide is produced when all of the propane in a typical propane tank is burned? Typically, a propane tank holds about 4.6 gallons of liquefied propane. Since it has a density of 4.11 pounds per gallon (0.493 g/cm3) that means that the tank holds 8.5 kg (8,500 g). The molar mass of propane is 44.096 g/mol so 8.5 × 103 g is 190 moles of propane. Clearly, the propane is the limiting reactant in this case since oxygen from the air is basically unlimited. So how many moles of carbon dioxide would be produced by burning all of the propane in the tank?
3 mol CO2
190 mol C3H8 × ---------- = 570 mol CO2
1 mol C3H8
Similarly, the amount of water that is produced depends only on the amount of propane burnt. So far so good. But what if the problem does not say which reactant is in excess? How can you decide which one it is?
The equation above shows what happens when copper metal is dissolved in nitric acid. How many moles of nitrogen monoxide gas (NO) are made when 2.00 mol copper (Cu) are placed in a solution containing 5.00 mol nitric acid (HNO3)? One reactant or the other will be used up first. When it is, the amount of product being made can no longer increase. If we calculate the amount of product expected for both reactants, then whichever one ends up making less was the limiting reactant. And the amount calculated for that reactant is the amount that is actually made.
Hypothetical Calculations:
2 mol NO
5.00 mol HNO3 × ----------- = 1.25 mol NO
8 mol HNO3
2 mol NO
2.00 mol Cu × ----------- = 1.33 mol NO
3 mol Cu
Since the calculation with the 5.00 mol HNO3 produced a smaller amount of the product, NO, it means that HNO3 was the limiting reactant. The amount of NO produced in the reaction is 1.25 mol.
The limiting reactant determines the maximum amount of product that can be made. It also determines how much of the other reactant, the excess reactant, is left over. How much copper is left over in this example? The amount of copper that reacted with the nitric acid is:
3 mol Cu
5.00 mol HNO3 × ----------- = 1.88 mol Cu
8 mol HNO3
Since 1.88 mol of copper are used in the reaction the amount of copper left over is:
2.00 – 1.88 = 0.12 mol Cu
It is often the case that limiting reactant problems will give only the masses of the reactants, not the number of moles. This is simple enough to handle: just convert all quantities to moles before calculating the amount of product expected for each one. In order to do this, you will need to calculate molar masses for the reactants and the product you use in your calculation. Here is an example to demonstrate the idea:
Calcium carbonate reacts with hydrochloric acid to produce carbon dioxide, water, and calcium chloride. If you have 2.50 g of calcium carbonate and a solution containing 0.100 moles of hydrochloric acid then how many grams of carbon dioxide would be produced?
The first thing to do is to write a balanced equation:
Next, calculate the molar mass of calcium carbonate and carbon dioxide:
CaCO3 1 × Ca + 1 × C + 3 × O 1 × 40.078 + 1 × 12.011 + 3 × 15.999 = 100.09 g/mol CO2 1 × C + 2 × O 1 × 12.011 + 2 × 15.999 = 44.01 g/mol
The number of moles of calcium carbonate can be calculated as follows:
1 mol
2.50 g CaCO3 × ---------- = 0.0250 mol CaCO3
100.09 g
Next, determine which reactant is the limiting reactant by calculating the grams of carbon dioxide you would get for both reactants, as if it were the limiting reactant:
Hypothetical Calculations:
1 mol CO2 44.01 g
0.0250 mol CaCO3 x ------------ x --------- = 1.10 g CO2
1 mol CaCO3 1 mol CO2
1 mol CO2 44.01 g
0.100 mol HCl x ------------ x ---------- = 2.20 g CO2
2 mol HCl 1 mol CO2
The idea of the limiting reactant is that it limits the amount of product you can make since you run out of one of the reactants before you run out of the other(s). In the example above, the calcium carbonate gets used up and there is some hydrochloric acid left over. You can tell this is the case in the problem by using each reactant to predict the amount of the product. Whichever reactant produces the smaller amount of product is the limiting reactant. In this case, the calcium carbonate (CaCO3) is the limiting reactant and the hydrochloric acid (HCl) is the excess reactant.
The calculation below will determine how much of the hydrochoric acid remains after the reaction is complete.
2 mol HCl
0.0250 mol CaCO3 x ------------ = 0.050 mol HCl was used in the reaction
1 mol CaCO3
So the amount left over can be calculated by subtracting this amount from the amount we started with, 0.100 mol HCl:
0.100 – 0.050 = 0.050 mol HCl is left over
Up to this point in the discussion of stoichiometry the assumption has been that all reactions go until the limiting reactant is used up. A chemist describes this by saying that the reaction goes to completion. When a reaction goes to completion it uses up all of the limiting reactant and makes only the products shown in the reaction of interest. For some reactions this is absolutely what is observed. When this happens the reaction is said to produce the theoretical yield. The theoretical yield is the maximum amount of product that can be made from a given amount of reactant chemicals. Up to now all the stoichiometric calculations you have done have resulted in an amount of product properly understood as the theoretical yield.
For the majority of chemical reactions it is not the case that the maximum possible amount of product is made. First of all, the written reaction under consideration may not be the only reaction that occurs. When this is the case the reactants participate in side reactions. Side reactions are chemical reactions which may or may not be known but which use up the same reactants as in the chemical equation that you are concerned with. They produce products other than the ones of interest. The consequence of this is that the amount of product actually made is less than the theoretical yield.
Secondly, chemical reactions may be subject to the condition of equilibrium. It may be that the most stable mixture of reactants and products is not one in which the reactants are used up completely to make products. Many chemical reactions are reversible: products can react to make the reactants again. When the equilibrium point is reached the reaction continues at the molecular level but appears to stop based on simple observation. Reactant molecules continue to become product molecules but they do so at the same rate that product molecules react to become reactant molecules. Equilibrium is an advanced topic in chemistry and is beyond the scope of this text. Nevertheless, it is an important contributor to the situation in which the theoretical yield of products is not achieved in experiment.
Lastly, if a chemical reaction is carried out under conditions that are not ideal then the full theoretical yield may not be achieved. For example, some reactions are more efficient at turning reactants into products at high temperatures and other reactions are more efficient at low temperatures.
When the amount of product is less than the theoretical yield it is possible to calculate a percent yield for the reaction. The percent yield is a measure of the efficiency of the reaction in producing the intended product. It is calculated by dividing the actual amount of product by the theoretical yield of product and multiplying by 100%. Here is an example:
In Example 1 the amount of nitrogen monoxide formed was 1.25 mol. This was the theoretical yield for that problem because it was calculated using the limiting reactant. If the experiment were performed in a lab and the actual number of moles of NO was found to be 1.00 mol then what was the percent yield?
1.00 mol ---------- × 100% = 80% 1.25 mol
The percent yield in this case was 80%. This means that only 80% of the theoretical yield was actually collected when the experiment was carried out. Either a side reaction used up some of the nitric acid or the equilibrium amount of NO is less than if the reaction were to go to completion.
Percent yields can also be calculated based on masses.
In Example 2 the theoretical yield of CO2 was 1.10 g. Say the experiment were carried out in a lab and the amount of CO2 was found to be only 0.78 g. In that case the percent yield is calculated as seen below:
0.787 g --------- × 100% = 71% 1.10 g
The following exercises were written in the order given to help you to develop the skills necessary to master limiting reactant, theoretical yield, and percent yield. You will need a calculator and a periodic table to complete them. You may also use your ions reference sheet.
Conceptual Questions | |
|
|
Introduction to Limiting ReactantN2 + 3H2Nitrogen gas reacts with hydrogen gas to synthesize ammonia gas. | |
|
|
Basic Limiting Reactant Problems5C + 2SO2Solid carbon reacts with sulfur dioxide to make carbon disulfide and carbon monoxide. | |
|
|
Limiting Reactant and Percent Yield Problems | |
|
|