In this lab students will measure the heat capacity of a metal sample and measure the molar heat of solution of potassium nitrate.
The scientific concept of energy is a difficult one. The basic idea is that energy is the capacity to do work or to oppose natural forces such as gravity or electric fields. This seems natural enough. But energy is actually a difficult idea because it is a mathematical abstraction which by definition always has the same value. No matter what happens, the amount of energy involved in an event is always the same after the event as it was before the event. In fact, the amount of energy in the entire universe is understood to be constant. Formally, this idea is called the First Law of Thermodynamics. We will use this law in order to understand and interpret our work in the lab. Simply put, all of the energy lost by one object plus all of the energy gained by another equals zero.
The trouble with the First Law is that it says nothing about what forms energy may take. For example, we all know that heat is a form of energy. Formally, the definition of heat is a form of energy and when added to a system the temperature of the system rises as long as the system is not undergoing a chemical or physical change. Heat is involved in chemical and physical changes as the energy released when bonds form and the energy absorbed when bonds are broken. Light is also a form of energy: when you sit out in the sun you can feel your skin become warmer and heat is certainly a form of energy. Also, perhaps from other science classes, we know that energy can be associated with motion, so-called kinetic energy. The faster something is moving, the more energy it is understood to have. Finally, in another invention of scientists designed to keep track of this slippery abstraction, there is the concept of potential energy. One form of potential energy is called gravitational potential energy and can be understood through the following example. A 1 kg rock raised one meter above the floor will strike the floor at nearly 10 mph (4.4 m/s) when dropped. The same rock when dropped from 10 meters above the floor will strike at nearly 30 mph (14 m/s). Clearly the rock had more energy—potential energy—when raised to 10 m than when it was only 1 m above the floor.
Because energy is understood to have many forms it can be a difficult thing to measure and keep track of for purposes of making measurements of changes in energy. If energy should assume a form that you did not anticipate you may find that some energy is apparently lost. Fortunately in this lab activity the work is designed so that all energy will be in the form of heat. Even so, some careful thinking is involved in keeping track of the origins and destinations of the heat in this lab. We will use the First Law as follows: The heat lost by one object is gained by the others in contact with it. We will measure these exchanges of heat by way of measuring temperature. Heat itself is not directly measurable and there is no such thing as a ‘heatomometer’. Fortunately, there is such a thing as a thermometer.
Though heat and temperature are not scientifically equivalent they seem to mean about the same thing to most people. The distinction between them is an important one, however, so we will explore it a bit here. In common speech heat and temperature are often interchangeable. “This cup of boiling water is hot,” means both that the temperature is high and that the water is full of heat. Although the former is true, the water does have a high temperature, the latter is not. A bathtub full of water heated to 37°C (body temperature) requires much more heat energy than a cup of water boiled for tea. Even cold water contains heat because if a colder material is placed in it, then heat will move out of the cold water and into the colder object. Heat does not have to be hot (that is, an object does not need to have a high temperature to have heat in it).
Temperature measures the average kinetic energy (which is related to the speed) of molecular motion. The higher the temperature, the faster the molecules in a sample of matter are moving. The lower the temperature, the slower the average speed of the molecules. When heat moves into a material it sometimes causes a change in temperature. Adding heat to a collection of molecules will cause their random motion to increase—the molecules will move faster on average than they did before heat was added. As long as no chemical reaction or phase change occurs this leads to a rise in temperature. When heat moves out of a system the average molecular speed is reduced. As long as there is no chemical reaction or phase change this leads to a drop in temperature. To be clear ‘cold’ is not a form of energy and cannot be added to something to cool it down. An object or the air in the room cools down as a result of the removal of heat energy and not because ‘coldness’ was added.
When two materials are placed in contact they will exchange heat only if they are at different temperatures. Heat naturally moves from the object with a higher temperature into the object with a lower temperature. Anyone can verify this who has held a cup of hot coffee: the heat from the cup moves into the hand holding it, causing it to become warmer—in other words, the temperature of the hand rises as the temperature of the cup falls. If two objects placed in contact have the same temperature then they will not exchange heat energy. If a piece of metal is placed in boiling water it will quickly have the same temperature as the water. When that same piece of hot metal is taken out of the boiling water and placed into cooler water it will lose a quantity of heat and cause the water to warm up. Formally, we can write an equation for this process. The equation below is only true if the exchange occurs in a closed system which is insulated against the loss or gain of heat by exchange with the surroundings.
Heat and temperature can be particularly confusing when chemical reactions or phase changes come into play. Heat added to a system can cause molecular motion to increase in speed but it can also be used to break bonds holding one molecule to its neighbor. Water molecules are held together in the solid and liquid form with a strong form of inter-molecular bond called a hydrogen bond. To break these bonds requires an input of energy and when heat is added to an ice cube it causes the water molecules to shake more violently and some of the heat energy is consumed in breaking hydrogen bonds. Under circumstances where the number of bonds broken equals the number of new bonds that form (a special condition called equilibrium) the temperature can remain the same even while heat enters the system. The heat is consumed in causing the phase change from a solid to a liquid: it breaks bonds instead of speeding up the molecules.
Even though the system’s temperature may remain the same, the temperature of the surroundings may drop. If the heat that drives the melting is coming from the counter-top in a kitchen then that counter-top will experience a drop in temperature. An endothermic process is one in which heat enters a system and is consumed. In the case of melting ice heat enters the system and its temperature remains constant while the temperature of the surroundings falls.
Heat can leave a system when new bonds form between molecules. As steam condenses the water molecules must slow down in order to approach one another without immediately bouncing off. Heat must leave the system for the temperature to fall enough so that this can happen. At a specific temperature it is possible to set up an equilibrium where just as many molecules condense as evaporate. In this case the temperature of the system will remain constant inside the system. When the molecules do manage to stick together they do so with a release of heat into the surroundings. This is similar to the way that a stretched rubber band releases energy when it is allowed to snap: bond formation releases energy. For example, if the water molecules stick together on the surface of a piece of glass then the glass will gain the heat energy and its temperature will rise. Heat exits the system but the system can remain the same temperature while the surroundings absorb the heat and experience a rise in temperature. An exothermic process is one in which heat exits a system.
In the study of the exchange of energy (a.k.a., Thermodynamics) a useful distinction is made between processes that release energy and those that absorb energy. When the system releases energy into the surroundings the process is called exothermic. When the system absorbs energy from the surroundings the process is called endothermic. Physical changes that are exothermic include the condensation of water and the freezing of water. In both cases heat must exit the system in order for the molecules to slow down enough for the forces that attract the molecules to one another to be able to act. As the bonds between molecules form, this also releases heat. That the freezing of a substance is exothermic may seem counterintuitive at first because we think of it happening in a cold box on top of the refrigerator. The reality is that the heat removed from the inside of that box is released at the back of the refrigerator: the coils on the back are noticeably warm to the touch. They are warm with the heat removed from the food and ice cubes inside. Physical changes that are endothermic include melting ice and boiling water. In both cases heat must be supplied from the outside. In the case of ice this may be by passive transmission of heat into the ice cube from a warm glass of water. In the case of boiling water heat must be constantly supplied by the stove burner in order for the boiling to continue. In both melting and boiling molecules must speed up, which requires an input of heat, and break bonds holding molecules together, which also requires an input of heat. Another endothermic physical change is the formation of a solution of certain salts. When these salts dissolve in water they absorb heat and the temperature of the solution drops compared to the original temperature of the water. This shows that there is a net absorption of energy in the process and more energy is used breaking bonds than is released in the formation of new bonds. One example of a salt which has an endothermic heat of solution is potassium nitrate (KNO3). Other salts may release energy when mixed with water, notably calcium chloride (CaCl2).
Chemical changes are either exothermic or endothermic based on whether more energy is released due to bond formation than is consumed in breaking old bonds or vice versa. Chemical changes that are exothermic include burning hydrocarbons and mixing certain acids and bases. The heat released by these reactions comes from potential energy stored in the arrangement of the atoms and molecules: when new bonds form this releases heat. Endothermic chemical changes include the reaction between baking soda and vinegar. Mix a little of these two chemicals together in a glass held in the hand and it is clear that it becomes cool to the touch. Energy is absorbed from the surroundings in order to break bonds. The newly formed bonds do not release as much energy compared with the energy used to break bonds. As a result, the mixture’s temperature drops.
Heat energy will be measured in joules (J) in this lab because J is the SI unit of energy. An older unit of energy is the calorie and it originates in the idea of specific heat since in units of calories the specific heat of water is 1 calorie/g·°C. This calorie is 1,000 times smaller than the Calories you are meant to fear as displayed on the Nutrition Facts labels on your food. Those Calories are really kilocalories. Heat is calculated mathematically based on the change in temperature of a substance, the mass of the substance, and a quantity called the specific heat of the substance. The specific heat (also called heat capacity) is a constant that quantifies the amount of heat required to raise the temperature of one gram of a substance by 1 degree (°C or K). The specific heat is different at different temperatures but for purposes of this lab we will assume that it is in fact constant over the temperature range we will encounter. The specific heat of water is 4.184 J/g·°C. Specific heat will be denoted as a lower-case letter ‘s’. By comparison with water, many other substances have much lower specific heats. Copper, for example, has a specific heat of 0.385 J/g·°C. In effect, much less energy is required to raise the temperature a certain mass of copper than to raise the temperature of an equal mass of water.
There is a simple equation that we will use to calculate the amount of heat involved in a change in temperature. It is the product of the mass of the substance, the specific heat, and the change in temperature. The change in temperature is usually written as ΔT and is defined as the final temperature minus the initial temperature: ΔT = Tfinal – Tinitial. So heat is calculated as follows for 1.00 × 102 g of water that experiences a rise in temperature from 25.0°C to 45.0°C:
This shows the amount of heat required to raise the temperature of 100 g of water by 20°C. If the substance had been copper instead the same temperature rise would have required only 770 J. Alternatively, if the 8.37 kJ had been used to heat 100 g of copper the temperature change would have been much greater: ΔT = 227°C! What follows is a pair of examples for the types of calculations you will carry out as part of analyzing your lab data.
A calorimeter is made using two nested styrofoam cups and filled with 175.0 g of water at an initial temperature of 25.0°C. A quantity of water is heated to 100.0°C and 25.0 g of aluminum is heated in the boiling water for five minutes. Once the aluminum has the same temperature as the boiling water it is removed with a pair of tongs and placed into the water in the calorimeter. What is the heat capacity of the piece of aluminum if the final temperature is 27.2°C?
For a calorimeter that we assume is perfect (it neither absorbs nor releases any heat) we can set up an equation showing that the heat lost by the metal plus the heat gained by the water equals zero:
This example was written so that the answer gives the accepted reference value for the specific heat of aluminum metal. Your work in the lab will involve a similar measurement but may not give a result that exactly matches the reference value. Differences may be due to heat lost in heating the calorimeter or due to the fact that a little hot water may have still been clinging to the metal when it was dropped in the calorimeter. The thermometer itself may be a source of heat or absorb some heat and play a role in determining the final temperature. Finally, inaccuracies in thermometer readings cannot be ruled out. Each of these will have a different effect on the outcome of your measurement, making it higher or lower.
Another example of an endothermic process is the formation of a solution of certain inorganic salts. Potassium nitrate (KNO3) has an endothermic heat of solution. This means that heat is absorbed from the surroundings to enable the KNO3 to dissolve. This leads to a reduction in temperature of the water and the vessel in which the solution is made. Heat has been used up and taken away from the water to create the solution.
Find the molar heat of solution for KNO3. First, dissolve 1.01 g of KNO3 in 25.0 g of water at 25.0°C. When this is done in a calorimeter which we assume neither absorbs nor releases heat the final temperature is 21.8°C
qKNO3 + qwater = 0347.9 J 101.1 g 1 kJ -------- * --------- * ------- = 34.8 kJ/mol 1.01 g 1 mol 1000 J
Note that the value for the heat of solution of KNO3 is positive. If you calculated the heat for the water it would prove to have a negative value. When solved for qKNO3 the equation gives a positive number. From the system’s point of view an exothermic process has a negative value for its calculated heat and an endothermic process has a positive value for its calculated heat. This comes about naturally from the basic equation for heat: q = sm(Tf – Ti). When Tf is greater than Ti then temperature increased (ΔT is positive). To raise temperature requires an input of heat. If heat is an input then a process is endothermic. The reverse is true when Ti is greater than Tf.
The following problems will help you to understand the concepts involved in this lab and to be able to do the math required for the analysis of your lab results.
The following list does not cover all possible hazards, just the ones that can be anticipated. Move slowly and carefully in the lab: haste and impatience have caused more than one accident.
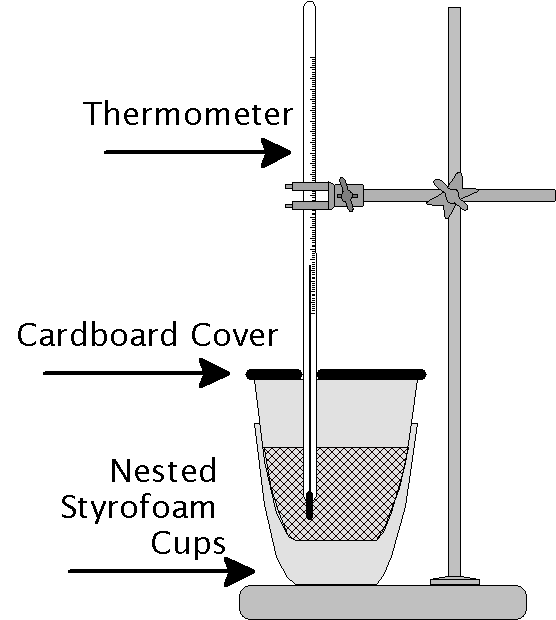
This lab has two main parts. First you will use the calorimeter to determine the specific heat of a sample of metal. In Part II you will measure the heat of solution of potassium nitrate. Ordinary table salt shows no change in temperature upon dissolving in water. Potassium nitrate on the other hand has a positive heat of solution, drawing heat from the water and reducing its temperature.
In this part of the lab you will use a simple constant-pressure calorimeter. Next you will heat a sample of metal in boiling water, which has a constant temperature. By placing the hot metal into the calorimeter and measuring the change in temperature you will be able to calculate specific heat of the metal.
In this part of the lab you will add a carefully measured mass (~3 g) of potassium nitrate (KNO3) to a calorimeter containing approximately 1 cm depth of water at a known temperature. Because this substance has a positive enthalpy of solution the temperature will drop as heat is removed from the water and calorimeter.
No formal lab report will be required. Instead make a data table for relevant data using a spreadsheet or word processing program. Then answer the following questions in a typed document. For calculations, show only the set-up and result. Do not show all intermediate algebraic steps.
Answer the questions in the analysis section of this lab handout (above) in a typed document.