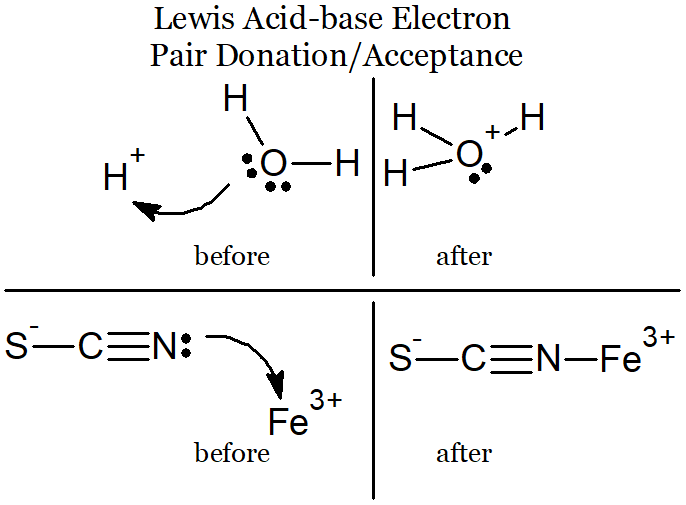| Stage |
Description |
How to calculate pH |
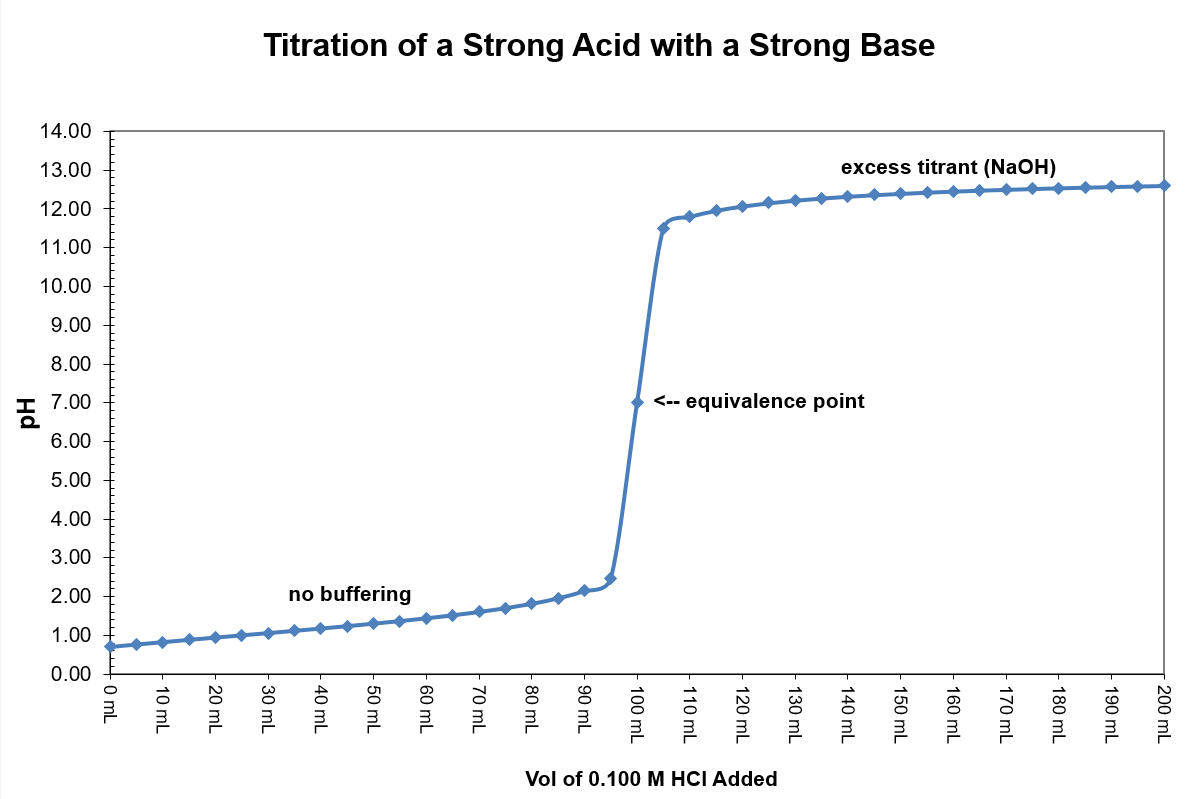
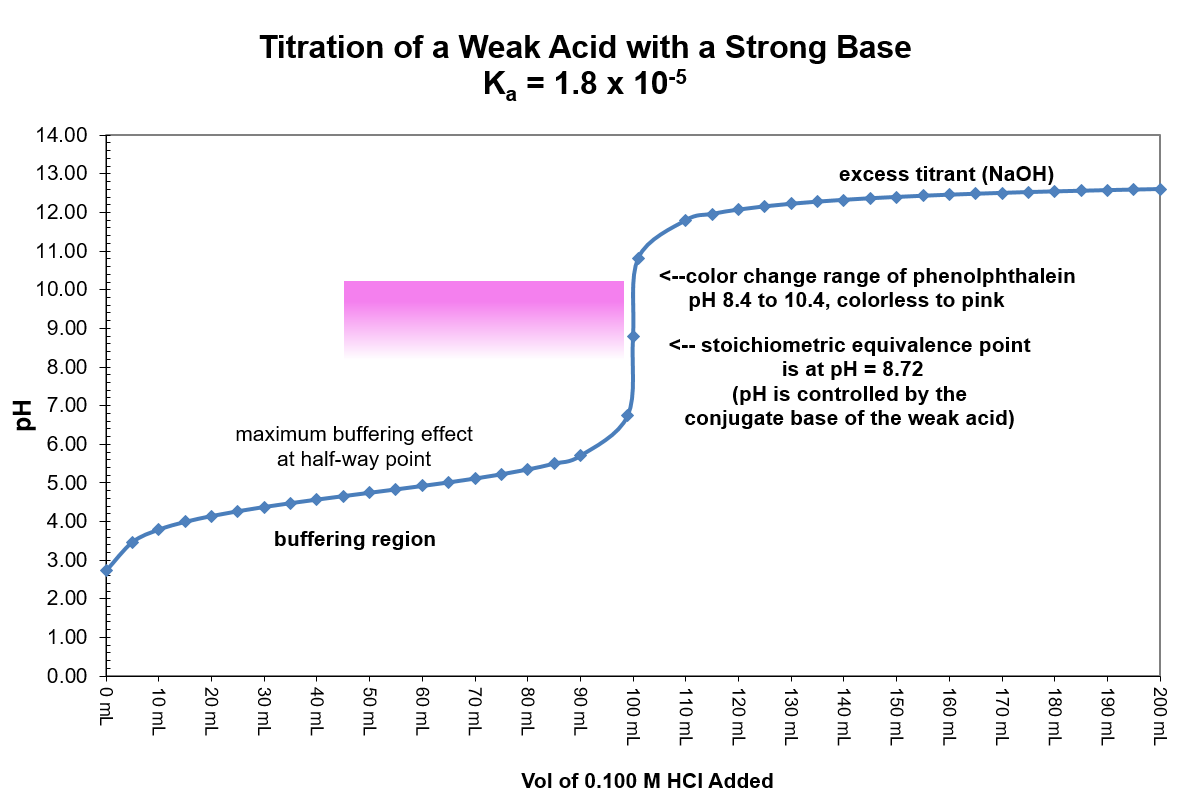
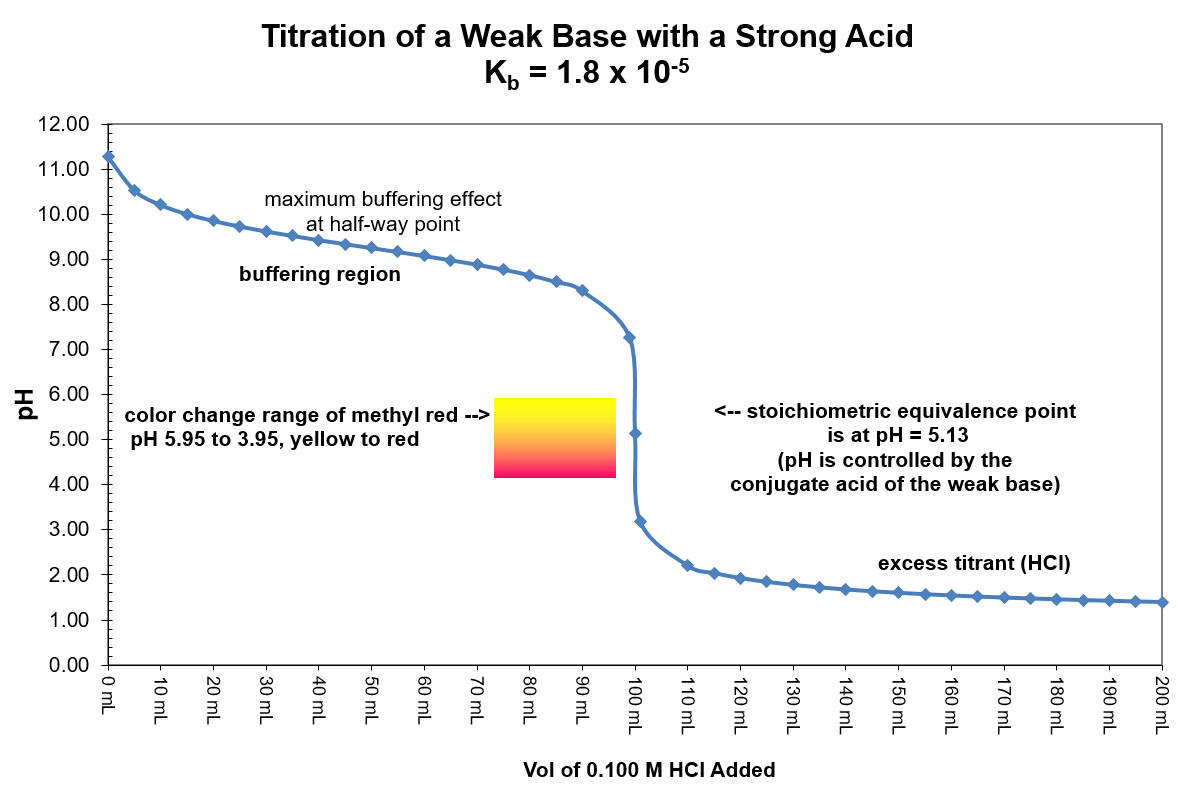
| Start |
Zero base added |
Solve HA ⇌ H+ + A– using the initial concentration of HA and an initial concentration of zero for H+ and A–. |
| Prior to Equivalence |
Any amount of added base up to but not incl. the stoichiometric equivalence point |
- Do stoichiometry calculation to determine how much HA is converted to A–.
([HA] = [(HA]0 – x)/(total volume) and [A–] = x/(total volume), where x is the number of moles of added base).
- Solve HA ⇌ H+ + A– using the new concentration of HA and the new concentration for A– leaving H+ as zero initially.
|
| At Equivalence |
The stoichiometric equivalence point where moles of base added equals the original moles of HA |
Now that all of HA has been converted to A– the relevant equilibrium is no longer the dissociation of the acid. Rather, it is the reaction of the conjugate base with water: A– + H2O ⇌ HA + OH–.
- Determine the number of moles of A– and the total volume; calculate [A–].
- Use [A–] and the equilibrium given above to find [OH–], pOH, and pH.
|
| After Equivalence |
An amount of added base that exceeds the number of moles of HA originally in solution |
Now that the amount of strong base added exceeds the original amount of the weak acid the pH is determined by the concentration of hydroxide ions. The conjugate base, A–, is a much weaker base and has no effect on the pH of the solution. Simply find the moles of excess OH–, divide by the total volume to find [OH–], calculate pOH, and pH = 14 - pOH.
|



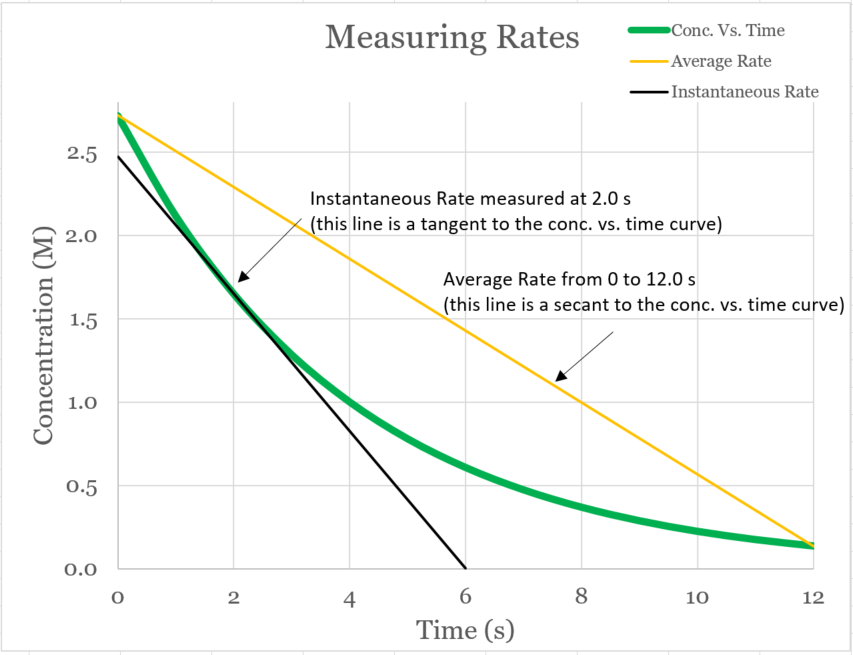
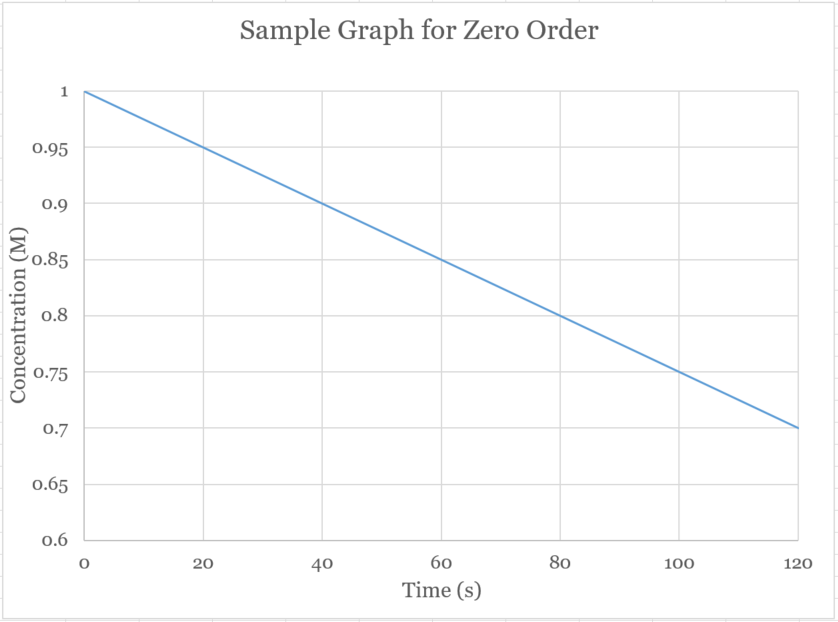
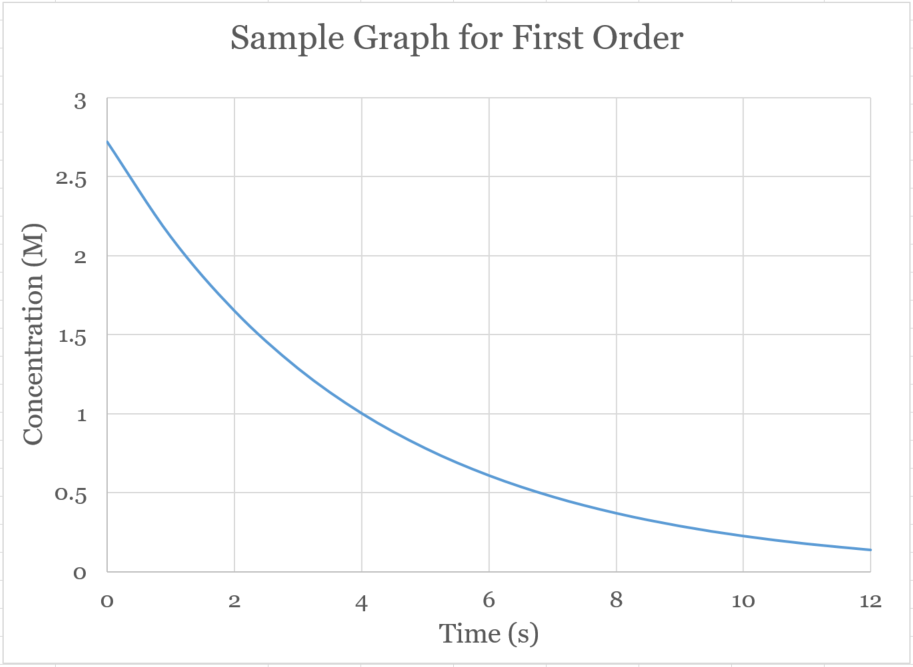
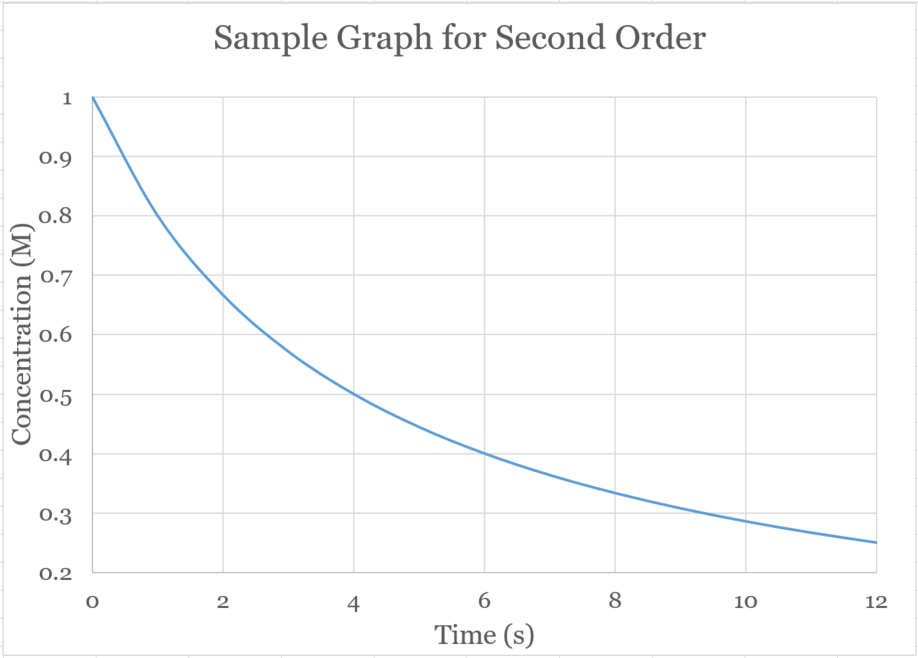
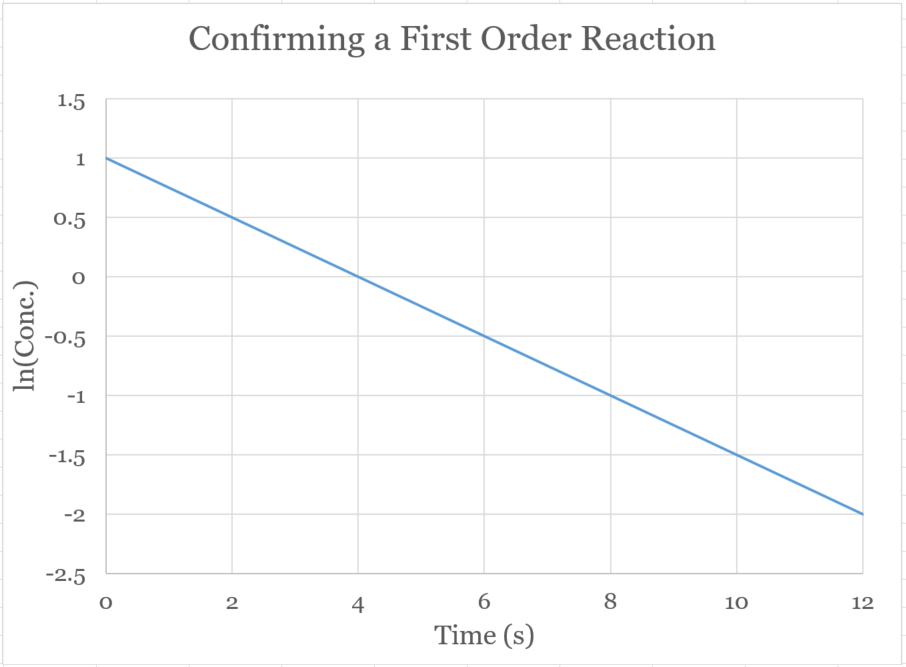
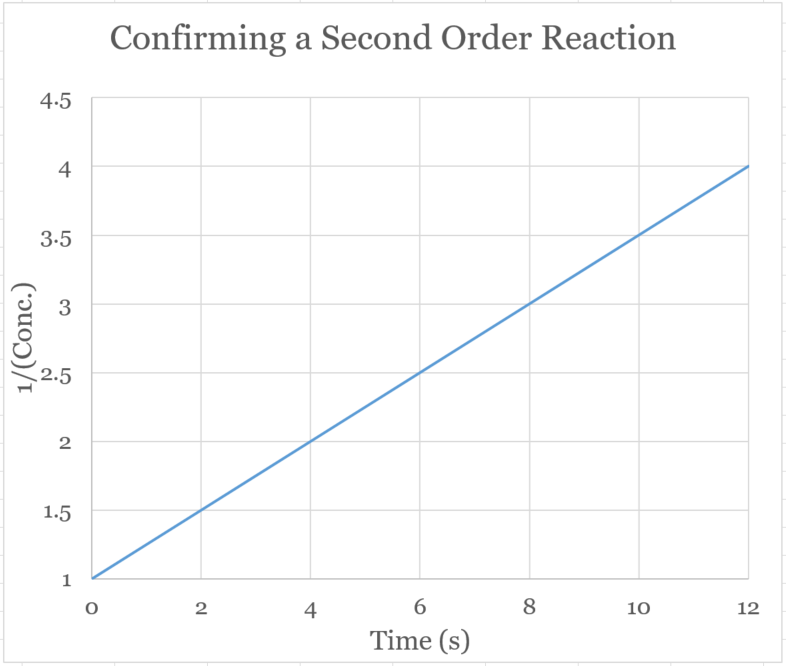
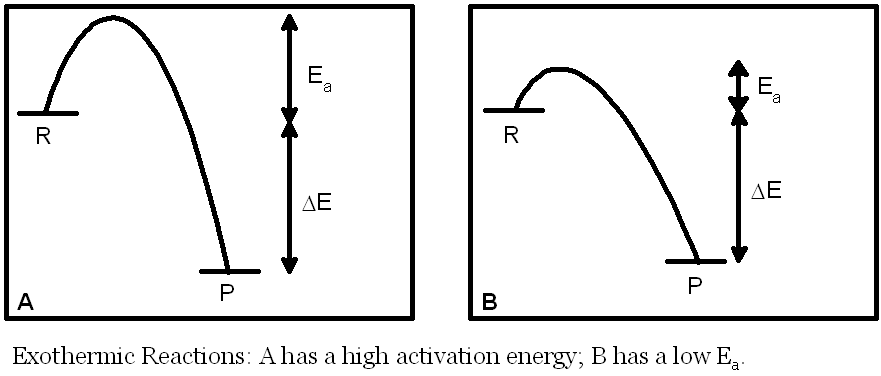
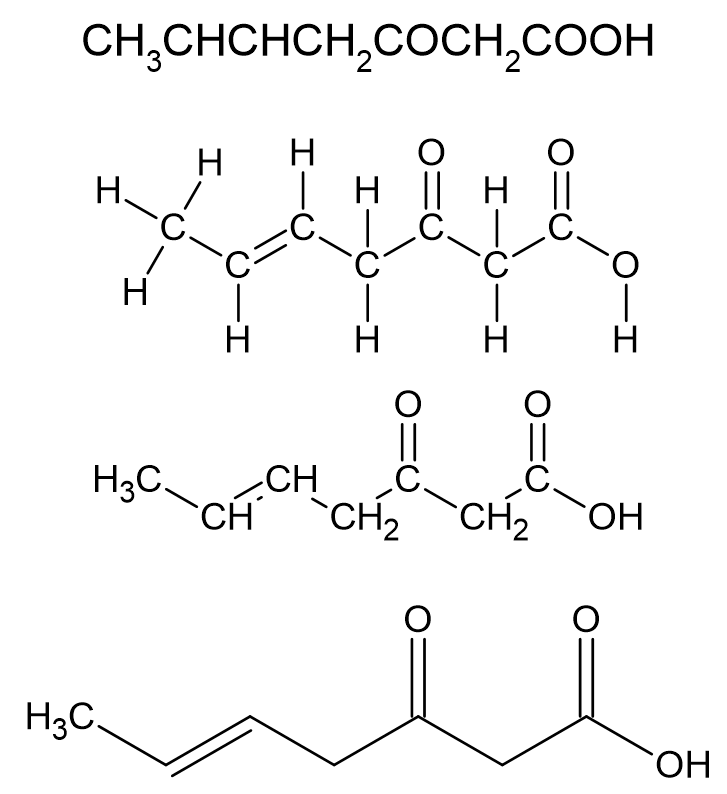
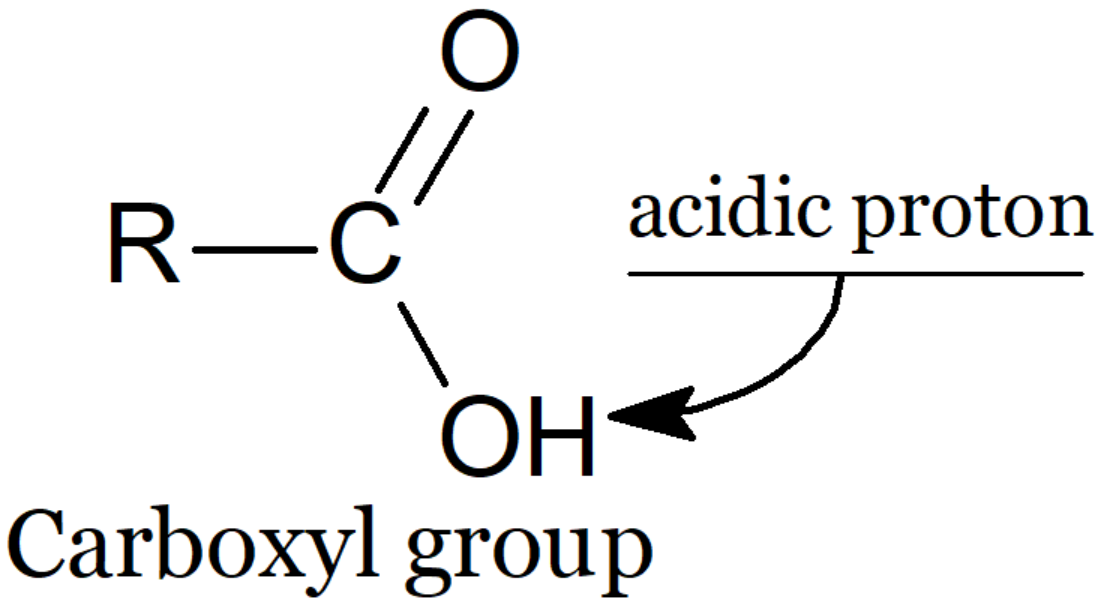 Know about organic acids, which contain a structure called a carboxyl group. They are collectively known as carboxylic acids.
Know about organic acids, which contain a structure called a carboxyl group. They are collectively known as carboxylic acids.