Group Activity: the Mole

Counting and Ratios

Atoms are the smallest pieces of chemical substances that there are. They come in different varieties called elements and although they can change their arrangements in uncountable ways, atoms themselves can be counted. In fact, counting atoms is central to the understanding of chemistry.

One way that counting is important in chemistry is that atoms can be counted in the ways they build up molecules. For example, molecules of oxygen, the gas that keeps us all alive, are made of exactly two atoms. That’s why the chemical formula for oxygen is O₂. Water molecules have exactly two atoms of hydrogen and one atom of oxygen: H₂O.

Atoms, or ions, are also counted in ionic compounds. The formula for such compounds does not give an exact number of atoms in each piece of the compound. Instead, there are at least two pieces to ionic compounds: a positive ion called a cation and a negative ion called an anion. Sodium chloride, common table salt, has the formula NaCl, which indicates that the ratio of sodium ions (Na⁺) to chloride ions (Cl^–) is one to one. Another ionic compound, copper (II) nitrate (Cu(NO₃)₂) has two nitrate ions (NO₃^–), which have four atoms each, for every one copper (II) ion (Cu²⁺). When ionic compounds dissolve in water and when they take part in chemical reactions they do so as separate ions so it’s important to bear in mind the number of ions that compose a compound.

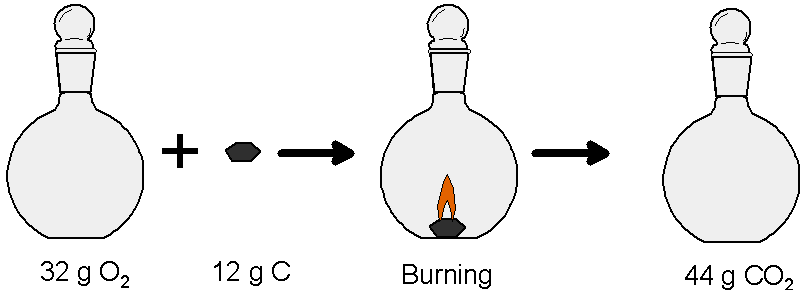
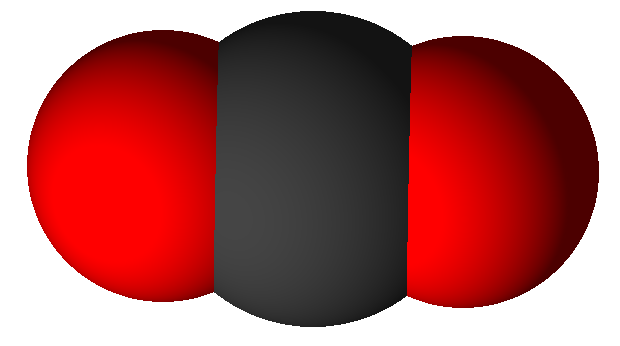
Another way that counting atoms is important is in chemical reactions. Balanced chemical equations describe chemical reactions by showing how atoms are rearranged in a chemical change while preserving the number of each kind of atom in the reaction. Reactants have bonds that are broken as they are transformed into the products, in which new bonds have formed. Two elements can often combine in different ways, with different numbers of atoms for each element. For example, carbon dioxide (CO₂) is made when equal numbers of carbon atoms (C) and oxygen molecules (O₂) combine. We say that they combine in a one to one ratio as seen in this chemical equation:

Carbon.dioxide.molecule-space-filling (26K)

Carbon dioxide
(CO₂)

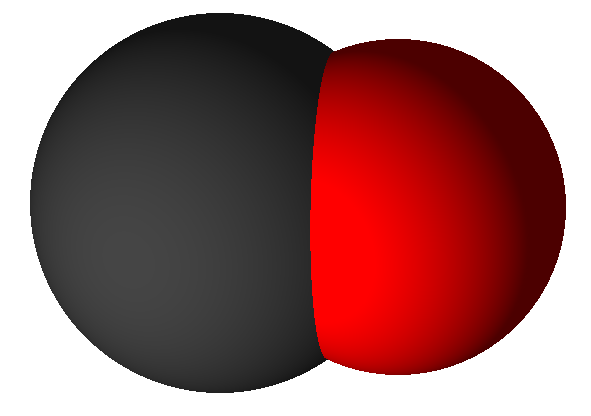
Carbon.monoxide.molecule-space-filling (25K)

Carbon monoxide
(CO)

C + O₂ → CO₂

In this equation oxygen reacts with carbon in a ratio of 1 oxygen molecule to 1 carbon atom.

Carbon can also combine to form carbon monoxide, an altogether different molecule. Carbon monoxide (CO) molecules have one atom of each kind. When carbon reacts with oxygen to make carbon monoxide it does so with half as much oxygen per carbon atom as when they combine to make carbon dioxide. That is, in a 1 oxygen molecule to 2 carbon atoms ratio, as seen in this chemical equation:

2C + O₂ → 2CO

These different ratios are rather abstract, but they are at the heart of our understanding of the fundamental laws of chemistry. Ratios by numbers of atoms and molecules are important in a practical sense, too. Carbon dioxide is a waste product of the way our bodies turn food into heat and the energy we need to think and to move. Our bodies also use it to maintain the correct pH in our blood, so it is an important molecule. Of course, if we breathe too much of it, carbon dioxide can harm us. Still, it’s a relatively harmless molecule with its ratio of one carbon atom for every two oxygen atoms. Carbon monoxide, on the other hand, with its one to one ratio, is a deadly poison. Even at very low concentrations it can cause death from a lack of oxygen. The carbon monoxide molecule binds to the oxygen-carrying proteins in red blood cells and keeps them from being able to transport oxygen.

Counting and Mass

The numbers of atoms per molecule and the ratios in which atoms combine in chemical reactions are clear and simple whole numbers. This is because atoms are objects that can be counted in whole numbers: there is no such thing as half of an atom. The problem is that atoms are so small and so numerous that we can never actually count them in the same way that you can count bananas or doughnuts. To see why, consider how many molecules of water (H₂O) there are in a tablespoon (about 15 mL). There are about

500,000,000,000,000,000,000,000 water molecules

This is far too many to count. Even counting 100 at a time, that is at 100 per second, it would take one and a half trillion centuries to count all of them! But if they are so numerous, and they can’t be counted, then where did this fantastic number come from? It came from the fact that it is possible to count things by weighing them. Consider the problem of ensuring that every ream of paper produced in a factory must have 500 sheets. One way the paper could be counted would be by weight. Given the average weight of a single sheet, 500 sheets would have a weight 500 times as big and so, without touching and counting each sheet, it is possible to know that there are 500 sheets.

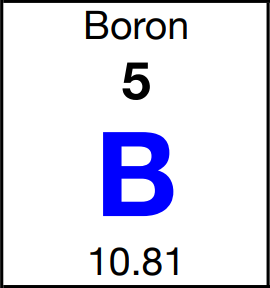
Atoms are counted by mass and it is interesting to see how this was set up. The starting point is the average atomic mass that is included in every box for every element on the periodic table. Boron, for example, has an average atomic mass of 10.81 amu. Atomic mass units (amu) are tiny units of mass used only for atoms and subatomic particles. They can be used to count small numbers of atoms. Ten atoms of boron would have a mass of 108.1 amu. One hundred atoms would have a mass of 1,081 amu. These are still very small numbers of atoms and masses too small to measure on a lab balance. By experiments that determine the number of atoms and molecules through chemcial reactions and the properties of gases, scientists are able to count atoms and to relate the number of atoms to the mass. And so it is possible to determine the conversion factor between atomic mass units and grams:

6.02 × 10²³ amu = 1 gram

The number 6.02 × 10²³ is called Avogardo’s Number. In the same way that 12 is the number of items in a dozen, Avogadro’s Number is the number of items in a chemical unit for counting items known as the mole. A mole is a group of items numbering 6.02 × 10²³. The word mole is a word used to represent a number, just like the words dozen, million, billion, or trillion. One mole of atomic mass units is equal to one gram.

1 mole of amu = 1 gram

This number is key to counting atoms in a practical way for laboratory work. Here is how it works. Find the mass of a mole of atoms in atomic mass units:

The mass per mole of boron atoms is,

  10.81 amu      6.02 × 10²³
 ——————————— × —————————————— = 6.5076 × 10²⁵ amu/mol
  1 B atom         1 mol

This number of amu is very large so in order to have a reasonable mass for a mole of boron atoms we will convert from amu to grams. A mole of boron atoms, that is, 6.02 × 10²³ of them, will have a mass we can work with:

Converted to grams, a mole of boron atoms has the mass,

 6.5076 × 10²⁵ amu        1 g
 ————————————————— × —————————————— = 10.81 g/mol
   1 mol B atoms     6.02 × 10²³ amu

This mass is a mass in grams for a large number of boron atoms, but instead of counting them individually, we count the atoms in groups. We count them in moles. The number 10.81 g/mol is the molar mass of the element boron. Molar mass is the mass in grams of one mole of a chemical substance, that is, it is the mass in grams for 6.02 × 10²³ molecules. The units are g/mol and so the molar mass is a conversion factor that allows chemists to calculate the number of atoms in moles given the mass of a sample in grams or to calculate the mass of a sample in grams given the number of items in moles.

Formula Weight and Molar Mass

In order to convert the mass of a chemical into the number of moles, which is a way of counting the number of items, it is necessary to calculate the formula weight. The formula weight is the sum of all of the masses of the atoms in a chemical formula. Here are two examples:

H₂O	(2 × H) + (1 × O)	(2 × 1.008) + (1 × 15.999) = 18.02
Fe(NO₃)₃	(1 × Fe) + (3 × N) + (9 × O)	(1 × 55.845) + (3 × 14.007) + (9 × 15.999) = 241.857

The final number for each chemical is the molar mass, which is a conversion factor for that chemical to convert between a mass and the number of items in moles. It is an unchanging characteristic for a chemical substance, just like the density, color, and melting point. The molar mass is used to find out how many items you have when you weigh a sample of a material or to calculate the mass for the number of moles you need for a specific experiment.

Molar mass is a conversion factor that turns a mass in grams into a number of moles or vice versa. This is valuable in the lab because the number of moles can’t be measured directly. Instead, chemists measure masses. So to find out how many moles of a chemical there are in a given mass, you use the molar mass to convert from mass to moles, as in the following example:

Example 1

You have a beaker that weighs 42.71 g. You add some water and the mass increases to 63.28 g. How many moles of water are in the beaker?

First, find the mass of water:
63.28 g – 42.71 g = 20.57 g of water
Second, calculate the molar mass of water:
(2 × 1.008) + (1 × 15.999) = 18.02 g/mol
Third, convert grams to moles using the molar mass:
                1 mol H₂O
 20.57 g H₂O × ---------- = 1.14 mol H₂O  
                18.02 g

On the other hand, at times a specific number of moles will be needed for an experiment or to mix a solution with a specific concentration. In that case, you convert the moles of the chemical that you need into a mass in grams, which it is easy to measure out in the lab.

Example 2

You need 2.5 mol of water for an experiment. To measure this you need to know how many grams of water this is.

First, calculate the molar mass of water (see ex. 1)
Second, use the molar mass to convert from mol to g
                 18.02 g
  2.5 mol H₂O × ---------- = 45.05 g H₂O 
                 1 mol H₂O

Counting Atoms within Molecules

The chemical formulas of molecules show the number of each type of atom found in the molecule. This number can of course be scaled up. For example, ten water molecules have a total of 20 hydrogen atoms, and 10 oxygen atoms. Similarly, 10 mol H₂O have a total of 20 mol H atoms and 10 mol O atoms. You can do this calculation as a sort of unit conversion by taking the chemical formula to count numbers of atoms within molecules according to their chemical formula. For example:

Example 3

   2 mol H                 1 mol O              1 mol O
-------------    and    -------------   and   -----------
  1 mol H₂O               1 mol H₂O              2 mol H

At times it is useful to be able to count atoms within samples of substances in the lab, where we rely on mass to measure things. Molar mass enables you to calculate the number of moles of hydrogen atoms there are in 75 g of water, for example:

Example 4

How many moles of hydrogen atoms are there in 75 g of water?

First, calculate the molar mass of water (see ex. 1)
Second, use the molar mass to convert from g to mol
            1 mol H₂O
75 g H₂O × ---------- = 4.16 mol H₂O  
            18.02 g
Third, calculate the number of hydrogen atoms in moles
                 2 mol H
4.16 mol H₂O × ----------- = 8.32 mol H atoms
                1 mol H₂O

Another way to use this idea is to calculate the mass of a single element that is present in the mass of a substance. Silver nitrate (AgNO₃) is a common laboratory chemical also used in the development of black and white photographic films and papers. If you wanted to calculate the mass of silver atoms in a supply of this chemical then you can use this idea of counting moles of atoms within molecules, as in this example:

Example 5

How many grams of silver (Ag) are there is 5.0 g of silver nitrate (AgNO₃)?

First, calculate the molar mass of silver nitrate:
(1 × 107.87) + (1 × 14.007) + (3 × 15.999) = 169.874 g/mol
Second, calculate the number of moles of silver atoms:
               1 mol AgNO₃      1 mol Ag
5.0 g AgNO₃ × ------------- × ------------- = 0.0294 mol Ag atoms
               169.874 g       1 mol AgNO₃
Third, calculate the mass of silver atoms:
                  107.87 g
0.0294 mol Ag x ------------- = 3.18 g Ag
                 1 mol Ag

Using Avogadro’s Number

Generally, chemists do not use Avogardo’s Number (6.02 × 10²³) very much. The whole point of it is to change numbers representing atomic mass units per atom to grams per mole so that atoms and molecules can be counted by weight. However, it is helpful in developing your understanding of the size of atoms and molecules. It is such a large number that it shows just how small atoms and molecules are in comparison to the objects we are used to in our lives. To help with this comparison, it is useful to imagine having a mole of ordinary objects like eggs, pennies, or grapefruits. If it were possible to have a mole of chicken eggs they would cover the entire surface area of the Earth…four miles deep. If you were rich enough to own a mole of pennies then they could be stacked in groups 400 pennies high in a disk that reaches from the surface of the Earth all the way to the orbit of the moon. (The bank teller would hate you for bringing them in for a deposit; it is enough money so that if distributed evenly every person on Earth would have over 1 trillion dollars.) Finally, how many grapefruits would it take to fill the entire volume of the Earth? The volume of the Earth is about 10²¹ m³. It takes about 500 grapefruit to fill up a box one meter on a side (1 m³). A mole of grapefruit would be large enough to fill the entire volume of the planet Earth. There is an excellent working out of the consequences of having a mole (the number) of moles (the small burrowing mammal) and you should read it: https://what-if.xkcd.com/4/.

As you can see, having a mole of anything that has a normal size is nearly inconceivable. There is another reason to use Avogadro’s Number, and that is anytime you need to know something like how many atoms are equivalent to the thickness of a hair or a piece of aluminum foil. Granted, these occasions are rare, but they do come up from time to time. Here is how to handle it:

Example 6

A calculation has determined that a piece of aluminum foil has a thickness made up by 1.08 × 10^–19 mol of aluminum atoms. How many individual atoms is this?

                   6.02 × 10²³
1.08 × 10^–19 mol × -------------- = 6.5 × 10⁴ or 65,000 aluminum atoms
		     1 mol

Example 7

In order to determine the number of atoms that cross the thickness of a piece of copper wire you might first calculate the number of copper atoms in a piece of wire. Find the number of copper atoms in 0.25 g of copper (Cu).

First, find the number of moles of copper atoms:
             1 mol Cu
0.25 g Cu × ---------- = 0.00381 mol Cu  
             63.546 g
Second, calculate the number of atoms using Avogadro's Number:
                   6.02 × 10²³
0.00381 mol Cu × ------------- = 2.30 × 10²¹ Cu atoms
		     1 mol

Example 8

How many grams of uranium (U) are there if you have 1.2 × 10²³ atoms?

First, find the number of moles of uranium atoms:
		        1 mol
1.2 × 10²³ U atoms × ------------ = 0.20 mol U  
                     6.02 × 10²³
Second, calculate the mass using the molar mass of uranium:
              238.03 g
0.20 mol U × ---------- = 47.6 g U
               1 mol

Comparing Numbers of Moles

It is important to remember that for the purpose of studying chemistry the important quantity is the number of moles, not the mass. It is the number of molecules reacting with each other that predicts the outcome, not the mass. For that reason it is valuable to have an understanding of relative numbers of particles. This can be counterintuitive, as the following example shows:

Example 9

Which sample has a larger number of particles? In other words, which one has a larger number of moles, 8.06 g of hydrogen (H₂) or 79.85 g of iron(III) oxide (Fe₂O₃)?

              1 mol
8.06 g H₂ × ---------- = 4.00 mol H₂
             2.01559 g
                  1 mol
79.85 g Fe₂O₃ × ---------- = 0.5000 mol Fe₂O₃
                 159.69 g

There are 8 times more particles of H₂ in 8.06 g than there are particles of Fe₂O₃ in 79.85 g. This may seem odd, that there are so many more molecules of hydrogen than units of iron(III) oxide. But it makes sense because hydrogen has a molar mass that is much smaller. Think of it this way, if you have 2 kg of coconuts than you have fewer nuts than if you have 2 kg of walnuts. And this is just because walnuts are so much smaller than coconuts.

page break

Questions and Problems

Comprehension Questions

Answer the following questions using one or more complete sentences. Show work for any calculations.

How is the counting of atoms important in understanding the composition of chemical compounds?
Why is counting atoms and molecules important for understanding chemical reactions using chemical equations?
Show how the mass in atomic mass units of a mole of carbon atoms can be converted into grams using the conversion factor given in the text.
How is a mole similar to a dozen?
How does the molar mass of a chemical relate mass to the number of molecules?
If you know how many moles of a chemical you have, and you know its chemical formula, how do you calculate the number of moles of each different type of atom in the chemical? For example, to the find the number of moles of chlorine atoms in a certain number of moles of iron(III) chloride (FeCl₃).
Why is it that there are more moles of aluminum atoms in 10 g of aluminum (Al) than moles of iron atoms in 10 g of iron (Fe)?

page break

Moles: Numbers and Masses

Molar Masses

For each of the following elements or compounds calculate the mass of 1 mole of particles of that substance. Express answers in units of g/mol.For example: the molar mass of HCO₃^– is H: 1 × 1.008 g/mol + C: 1 × 12.01 g/mol + O: 3 × 16.00 g/mol = 60.02 g/mol

See the Formula Weight section in the text.

Al
O₂
NaCl
H₂O

CaCO₃
AlPO₄
Mg(OH)₂
Fe₂(CO₃)₃

Putting Molar Masses to Work

The previous exercise requires you to find the mass in grams of one mole of a chemical substance. This mass has a special name in chemistry: the molar mass. When you work with this number, as with any number in science, you need a unit. The unit of molar mass is grams per mole (g/mol). To have a mole of sand (SiO₂) you measure out approximately 60 g. But chemists seldom work with exactly one mole.

How many moles of SiO₂ are there in 12 g? How many grams do you weigh out if you need 2.4 moles of SiO₂? Just use dimensional analysis to figure it out:

            60 g                              1 mol
2.4 mol × -------- = 144 g           12 g × -------- = 0.20 mol
            1 mol                             60 g

In the following problems, find the number of moles given the number of grams. Find the number of grams given the number of moles. See examples 1 and 2.

47 g of O₂
112 g of NaCl
91 g of H₂

14 mol of H₂O
0.35 mol of Fe₂O₃
42 mol of Mo(PO₄)₂

page break

Comparing Numbers of Particles

Write an equal sign (=), a greater than sign (>), or a less-than sign (<) between each of the following pairs. Determine which sign is appropriate by comparing the number of moles of each member of the pair. That is, compare the number of atoms or molecules in each member of the pair. For example, there are more atoms in 28 g of N₂ than in 2 g of C. This is because 1 mole of N₂ has a mass of 28 g. One mole of C has a mass of 12 g. Since there are only 2 g of C and this is equal to 0.17 mol there are more molecules of N₂ in 28 g of N₂ than in 2 g of C.

See example 9.

13.5 g Al 2 g He
10 g Fe 10 g Br
64 g NaCl 32 g H₂O
14 g Fe₂O₃ 14 g U

207 g Au 207 g Pb
1 g O₂ 1 g N₂
10 g H₂ 10 g PbCl₂
12 g H₂O₂ 11 g CH₄

Counting Atoms

Answer the following questions by performing a calculation. See examples 3, 4, and 5.

How many moles of Cl atoms are in 1 mol of MgCl₂?
How many moles of N atoms are there in 0.75 mol of Al(NO₃)₃?
How many moles of C₃H₈ contain 3.5 mol of hydrogen atoms?
How many moles of Fe₂O₃ contain 0.27 mol of oxygen atoms?

How many moles of potassium atoms are in 58 g K₂S?
How many moles of oxygen atoms are in 100 g O₂F₂?
How many moles of oxygen atoms are in 15 g H₂SO₄?
How many moles of H₂O contains 42.0 g of hydrogen atoms?

page break

Big Numbers

Answer the following questions by performing a calculation. You will need to use Avogardro’s Number (6.02 × 10²³ per mole) for every question. See examples 6, 7, and 8.

How many individual units of sodium chloride are in 2 mol NaCl?
How many individual units of iron(III) oxide are in 1.5 mol Fe₂O₃?
How many moles are there if you have 2.3 × 10²³ atoms of lead (Pb)?
How many moles of water are there if you have 4.2 × 10²² molecules?

How many individual units of sodium chloride are in 42 g NaCl?
How many individual units of iron(III) oxide are in 84.0 g Fe₂O₃?
How many grams of C₃H₈ is equal to 3.1 × 10²³ molecules?
How many grams of H₂O is equal to 5.4 × 10²⁵ molecules?

Introduction

In your everyday life you deal with groups of things. In chemistry you deal with groups of atoms and molecules. You put on a pair of socks in the morning. In the afternoon you might go out and buy a six-pack of soda. Your teacher goes through a dozen eggs about every five days. In the chemistry lab you might find it a bit harder to characterize the number of atoms or molecules that participate in a reaction.

In this lesson we will discuss how to come to grips with the vast numbers of extremely tiny particles that do the evaporating, condensing, reacting, and dissolving in the study of chemistry. For example, the tiniest speck of dust that you can see without a magnifying glass or a microscope is built of about 1 × 10¹⁶ atoms. An 8 oz. glass of water contains about 8 × 10²⁴ water molecules. There are more carbon atoms in the lead of your pencil than there are stars visible in the night sky.

Conservation of Atoms

You are familiar with the conservation of mass in chemical reactions. The conservation of mass is the direct result of the conservation of individual atoms and molecules. In a chemical reaction atoms and molecules become reorganized. They never disappear or become converted completely into energy.

The fact that atoms are never destroyed can have important consequences. For example, climate change due to the emission of carbon dioxide through the burning of fossil fuels is a direct result of the rule that atoms cannot be destroyed. Carbon compounds in the form of petroleum and natural gas are excellent fuels. Hydrocarbons (compounds that are made of C and H) release a lot of energy when those compounds are burned. This is because carbon and hydrogen have a chemical affinity for oxygen that is very strong.

When plain carbon burns, say in the form of charcoal, the reaction is written this way:

C + O₂

CO₂

This symbolic notation tells the love story of carbon and oxygen. Under the right conditions (say, in a well-burning, well-ventilated charcoal grill) carbon combines easily with oxygen and releases quite a bit of heat in the process. Perhaps disappointingly for some, this love story is a romance by the numbers. It says that every individual carbon atom always combines with exactly two oxygen atoms—one oxygen molecule. (Notice that the oxygen does not appear as a single atom but as a diatomic molecule: it nearly always does). Furthermore, the chemical equation shows that this process always results in exactly one molecule of carbon dioxide.

The power of the equation is not really obvious from this notion of single atoms and molecules. In the real world we never deal with atoms and molecules one at a time (there isn’t a pair of tweezers small enough). Instead we always have billions upon billions upon billions. So the equation really shows how useful it is when you consider that it says that no matter how many carbon atoms you have they will always react with as many oxygen molecules as there are carbon atoms.

Well, actually, that was a simplification. (The teaching of science is full of simplifications). Carbon and oxygen can work things out a different way if conditions require it. Under normal circumstances, when there is plenty of oxygen around, carbon will always combine with oxygen to form carbon dioxide. But when there is not enough oxygen, such as when someone runs a gas-powered electricity generator in a closed-up space, something much less romantic happens. Instead of making relatively harmless CO₂ the reaction becomes:

2C + O₂

2CO

Carbon dioxide is bad enough, considering the damage it is doing to the climate as a result of our insatiable energy requirements. Even so, it is relatively harmless in low concentrations. But CO (carbon monoxide) is downright hazardous.

Carbon monoxide binds to the oxygen-carrying protein hemoglobin in the blood 200 times more strongly than oxygen. When present, it prevents oxygen from binding to hemoglobin and this prevents it from reaching the body’s tissues. At a level of just 100 parts per million by volume in air it can cause dizziness and headaches. When its concentration reaches 667 ppm it can be fatal. The moral of the story: never run a generator (or burn charcoal) in an unventilated room.

Incidentally, take notice of the fact that both equations for the burning of pure carbon are what are called balanced chemical equations. A balanced chemical equation has exactly the same number and kinds of atoms before and after the arrow. In other words, the number of atoms that react (the reactants) is the same as the number of atoms the are produced (the products). This is really an expression of the Law of Conservation of Matter For example, there is one atom of carbon and there are two atoms of oxygen on both sides of the equation showing the product CO₂.

Conservation of Matter

Atoms and molecules are unimaginably small: a CO₂ molecule is about 0.29 nm long. That is 0.29 billionths of a meter long or 0.29 millionths of a millimeter. Written in decimal notation the length of the molecule is 0.000 000 000 29 m. Their masses are also incredibly tiny: a single molecule of O₂ has a mass of 5.3 × 10^-23 g. No lab balance ever made could possibly measure such a tiny mass. The amount of air you breathe in for each breath is about 0.5 L. This is actually a staggeringly large number of gas molecules: about 1.2 × 10²². Normal amounts of everyday materials are made of many, many incredibly tiny particles.

Because atoms and molecules are so small the only way to count them is to figure out a relationship between their mass and how many there are. In this way we can count them by weighing them. To do this we use correct chemical formulas and balanced chemical equations. Chemical formulas and equations relate numbers of atoms to each other based on how they bind to each other and react. By knowing their atomic masses and measuring the masses we work with the in the lab we can use chemical formulas and equations to count atoms. Here’s how:

Carbon monoxide results from burning fuel without enough oxygen. So how much oxygen do you need to make sure that all the carbon burns to form CO₂ and not to form CO? This is a question chemistry can help us to answer. We know that in a balanced chemical equation the number of atoms that react are the same as the number of atoms after the reaction is over.

C + O₂

CO₂
(reactants—one carbon atom and two oxygen atoms— react to make
products—a compound made of one carbon atom and two oxygen atoms)

We also know that one atom of carbon has a mass of 12 amu and that one molecule of oxygen (2 × 16 amu) has a mass of 32 amu. So the answer is that it takes a mass of 32 amu of oxygen to react with 12 amu of carbon if 44 amu of CO₂ is the product. To summarize: because we know that atoms are not created or destroyed, and we know the masses of those atoms, we know the mass of oxygen necessary to react with a given mass of carbon: 32 amu of oxygen for 12 amu of carbon, a ratio of ⁸/₃.

The ratio ⁸/₃ is a ratio of masses. That means that for any size mass of carbon you can figure out how much oxygen you need (by mass, if not by number of molecules). So say you have exactly 12 g of carbon (grams can be measured using a simple lab balance; atomic mass units are not so easy to measure). That means that you need 32 g of oxygen to react with it to make carbon dioxide: 12 g × ⁸/₃ = 32 g. By putting oxygen into a container of known mass sitting on a balance you can measure out 32 g of the gas. If you ignite the 12 g of carbon inside the container holding 32 g of oxygen they will both be used up and the container will then be filled with carbon dioxide.

Take notice of what just happened here. The ratio of masses depends on the idea that an individual carbon reacts with exactly one oxygen molecule. That is, because you know how many atoms of each element react you also know what mass of each element reacts. By using the ratio of the masses you can figure out what measurable mass, in grams, of each element will be needed for the reaction. So by weighing out twelve grams of carbon and 32 grams of oxygen you have in effect guaranteed that there are the same number of carbon atoms in twelve grams of carbon as there are oxygen molecules in 32 grams of oxygen. Another way to say it is this: The ratio of the number of particles is 1 O₂ to 1 C. The ratio of masses that matches this ratio of numbers is 32 amu/12 amu (8/3). If you take the same ratio of masses in grams (32 g/ 12 g) then the ratio of the number of particles must also be the same. Therefore the number of molecules of oxygen is equal to the number of atoms of carbon for 32 g of oxygen and 12 g of carbon. This result is very important because it shows how it is possible to count atoms and molecules by weighing them. The mass of a chemical sample is proportional to the number of atoms or molecules of that sample.

The Mole

Chemists have to deal with astonishingly small sizes and inconceivably large numbers if they want to understand what is going on in chemical reactions and physical changes. They do it by the simple method of weighing in order to count things. If you go to the hardware store to buy nails there is a good chance that they will weigh your purchase and not count each individual nail. If you have a stack of paper and you want to know how many sheets you have the simplest way to find out is to weigh the stack and divide by the weight of one sheet.

In the same way chemists use the mass of a pile of atoms or molecules to figure out how many atoms or molecules are there. They take one more step to simplify things even further. Chemists use a unit called the mole to keep track of the number of atoms or molecules. The mole is a unit like the dozen, the pair, the six-pack or the ream (a ream of paper is 500 sheets). There are twelve things in a dozen, two in a pair, six in a six-pack and 500 in a ream.

How many things are there in a mole? There are as many things in a mole as there are carbon-12 atoms in exactly 12 g of pure carbon-12. This definition alone would be enough for the mole to be a useful unit since carbon can be reacted with other elements and compounds, the results analyzed and in this way the mass of a mole of other chemicals can be determined. The number of things in a mole is a fundamental constant and has the value: 6.02 × 10²³/1 mol. The unit is in the denominator to reflect that this is the number of things per mole.

A mole is a collection of 6.02 × 10²³ items. In theory, you could have a mole of any kind of thing. A mole of water molecules has the same number of items as a mole of elephants. The elephants take up a lot more space, however. But the point is not really how many items there are in a mole. The point is what the mole can do. We saw earlier that 12 g of carbon and 32 g of oxygen have the same number of particles. These numbers were not selected at random: they are the mass of one mole of each of those substances.

For any singular atom or molecule it is easy to figure out the mass measured in atomic mass units (amu). The mass of a CO₂ molecule is 12 amu + 2 × 16 amu = 44 amu. The mass of an O₂ molecule is 2 × 16 amu = 32 amu. The mass of a single unit of NaCl is 23 amu + 35 amu = 58 amu. The great thing about the mole is that there are a mole of atoms or molecules in the mass of a substance in grams that is equal to the mass of a single unit of that substance in atomic mass units. In other words, there is a mole of CO₂ molecules in 44 g of CO₂. Likewise, 32 g of O₂ is a collection of a mole of oxygen molecules. Similarly, if you measure out 58 g of NaCl you have, at the same time, counted out a mole of NaCl units.

It is interesting to play around with the number of things in a mole to see just how big of a number the it is. If it were possible to have a mole of chicken eggs they would cover the entire surface area of the Earth…four miles deep. If you were rich enough to own a mole of pennies then they could be stacked in groups 400 pennies high in a disk that reaches from the surface of the Earth all the way to the orbit of the moon. (The bank teller would hate you for bringing them in for a deposit; it is enough money so that if distributed evenly every person on Earth would have over 1 trillion dollars.) One more illustration: the volume of the Earth is about 10²¹ m³. It takes about 500 grapefruit to fill up a box one meter on a side (1 m³). So a mole of grapefruit would be large enough to fill the entire volume of the planet Earth.

For many people the mole is a difficult concept. Perhaps this illustration might help. Say you have a dozen crocodiles and a dozen mice. There are twelve of each animal but you could never say that the two groups of animals have the same mass. It would only take one crocodile one snap of its jaws to consume the dozen mice! On the other hand, if you have 1,000 kg of crocodiles and 1,000 kg of mice you would have the same mass of each one. But you would certainly not have the same number of each animal. How many mice (weighing in at 25 g) would that be? A single average adult crocodile might have a mass of 1,000 kg.

To summarize: The mole is a quantity used by chemistry to count atoms, molecules, and particles of all kinds. The number of items in a mole is called Avogadro’s number and equals 6.022 × 10²³ per mole (/1 mol). The most useful aspect of the mole is that it relates the atomic mass of atoms to a measurable mass in grams. Specifically, a mole of any chemical substance has a mass in grams equal to the sum of the atomic masses of its atoms. For example, 1 mol of C has a mass of 12.011 g and 1 mol of KCl has a mass of 74.55 g.

page break