In this lesson you will learn about the four fundamental forces of nature and how two of them determine whether an isotope is stable or unstable. Stable isotopes do not decay or change over time. Unstable isotopes produce radiation and are transmuted into different isotopes and different elements. You will learn more about radiation in another lesson.
In modern physics there are four forces which, taken together, explain all possible interactions between pieces of matter. The forces are called Gravity, Electro-magnetism, the Strong Nuclear Force, and the Weak Nuclear Force.
You are probably already familiar with Gravity since it is the force that keeps you from floating up out of your chair. Gravity is an attractive force between two objects with mass. The strength of gravity depends on the size of the two masses and the distance between them. Gravity acts over all distances but its strength drops off with the square of the distance between two objects. That is, if something is twice as far from the Earth then it will feel a force only 1/4 as great. Gravity never has a repulsive effect. Gravity is responsible for keeping the Moon in orbit around the Earth and the Earth in orbit around the Sun. Gravity is only really important for objects with large masses: its effects are unmeasurable on the scale of atoms and molecules.
Electro-magnetism is more complicated than gravity. We will concentrate on just the electric part of this force. Electric forces are much stronger and more versatile than gravity. For example, the force of gravity between two protons in the nucleus of an atom is about 1 × 1036 times weaker than the electric force between the same two protons.
| Electric Forces | ||
| + |
||
| + >–< – | ||
| – |
||
Electric forces can be attractive or repulsive (see table at right). As you have seen in the lab, two objects with the same charge repel each other: they push one another away. On the other hand, two objects with opposite charges are attracted to one another. This is where the expression that ‘opposites attract’ comes from. Scientific investigations of electric forces led to calling one kind of charge positive and the other kind negative. Objects with all the positive and negative charges balanced out are called neutral and have a charge of zero. If two charges are positive (or if they are both negative) they will be repelled from one another. But if one charge is positive and the other is negative they will be attracted to each other. Incidentally, it is because of electric forces that you do not fall through the floor and that you cannot push objects right through each other. The electric forces that bind atoms together are very strong and cannot be broken easily.
The Strong Nuclear Force is what holds atomic nuclei together. It is a force that is always attractive like gravity but it can only work over extremely short distances: from 1.3 × 10-15 m to 2.5 × 10-15 m. For purposes of this activity it is enough to note that the strong nuclear force acts to make two nucleons attract one another inside an atomic nucleus. The word nucleon stands for either a proton or a neutron, both of which are found in atomic nuclei. This means that the strong nuclear force causes protons to be attracted to protons and neutrons and causes neutrons to be attracted to protons and neutrons.
The Weak Nuclear Force is not really important for the purposes of this lesson. It governs certain kinds of radioactive processes and is important for describing how radioisotopes (radioactive isotopes) decay. Radioisotopes are isotopes of an element that are unstable because of unbalanced forces in the nucleus of that isotope.
There are two kinds of subatomic particles in atomic nuclei. There are positively charged protons and neutrally charged neutrons. The protons are repelled from one another due to electric forces but neutrons are unaffected. Since they are so close together in the extremely tiny atomic nucleus the repulsive electric force is very, very high. If no other forces were acting then atomic nuclei could not hold themselves together. All the protons, since they are all positively charged, would push each other as far away as possible.
The strong nuclear force makes protons and neutrons stick together. It is not quite strong enough to make two protons stick together. The electric repulsion is stronger. But if there is also at least one neutron then the strong nuclear force can balance out the electric repulsion. This works because neutrons are not repelled or attracted by electric forces. They do respond to the strong nuclear force and can help hold atomic nuclei together. For example, take a nucleus with two protons and one neutron. The protons are electrically repelled but the neutron is neither repelled nor attracted. The strong nuclear force acts on all three particles to cause them to be attracted to one another. The neutron contributes just enough extra strong nuclear force to enable the nucleus to hold together. The protons are attracted to each other, too, but without the contribution of the neutron that attraction is not enough to keep the nucleus from being unstable. By the way, what element was used in this example?
Isotopes can be stable or unstable. Their stability depends on the balance of forces. If either the electric repulsion or the strong nuclear force is stronger than the other then the isotope will be an unstable radioisotope. A simple way to think about nuclear stability is to consider the ratio of the number of neutrons to the number of protons. Every isotope has some number of protons and some number of neutrons (sometimes the number is zero). The protons alone will not stick together to make an atomic nucleus. Some number of neutrons is necessary to provide enough strong nuclear force to balance the electric repulsion.
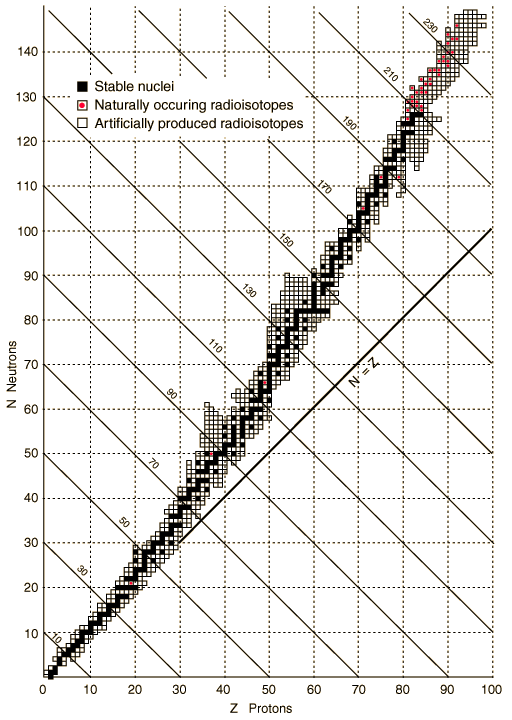
All of the known isotopes of all of the elements can be shown in a table of isotopes, as your teacher has already shown you. In the graph shown at left all of the isotopes are depicted as small squares placed to show the number of protons (x-axis) and neutrons (y-axis) in each one. There is a line on the graph showing the places on the graph where the number of neutrons equals the number of protons (n0 = p+ or N = Z). In these places the n0/p+ ratio is 1.
Some stable isotopes have a n0/p+ ratio close to one but as you add more and more protons the ratio gets larger because more neutrons are needed to provide enough strong nuclear force. Different elements have different stable ratios of neutrons to protons but if they do not have just the right ratio, they will be unstable.
Unstable isotopes decay by breaking up or by emitting particles or energy. Most of the unstable isotopes on this graph only exist when they are manufactured in a lab (the empty squares). These radioisotopes decay so rapidly that if they are made by natural processes they are not observed because they have already transmuted into other isotopes by the time scientists come across them. Even though the n0/p+ ratio of some isotopes is not ideal they occur in nature (the squares with dots). These naturally occurring radioisotopes are unstable but do not decay too rapidly and so can be mined from minerals on Earth. Examples include 40K (0.012%, t½ = 1.248 × 109 yrs), 48Ca (0.187%, t½ > 4 × 1019 yrs), 235U (0.7204%, t½ = 7.038 × 108 yrs), and 238U (99.2742%, t½ = 4.468 × 109 yrs).
There are several kinds of radioactive decay. Radioactive decay is a
process that unstable nuclei undergo in order to become more stable.
Usually it involves the emission of one or more subatomic particles from
within the nucleus. To emit means to send out or give off. One kind of
nuclear decay is called alpha decay and is symbolized by
the Greek letter alpha: α. Alpha decay occurs in atoms with a very
large atomic mass number (greater than 209). In these nuclei the strong
nuclear force runs up against the limitation that it only works over short
ranges. It literally can’t reach far enough to overcome the electric
repulsion of the protons in the nucleus. Alpha decay is a kind of
spontaneous fission in which a nucleus splits into two pieces. In this
case the nucleus splits into a large piece and a helium-4 nucleus. The
large piece ends up with a mass number 4 units smaller and an atomic
number 2 units smaller. A → (A - 4) and Z → (Z - 2). An
example reaction looks like this:
22288Ra →
4 2He2+
+ 21886Rn
Another kind of radioactive decay is called beta
decay. It is symbolized by the Greek letter beta: β. This
kind of decay occurs when there are too many neutrons in a nucleus for it
to be stable (the n0/p+ ratio is too high). In other
words, it happens when the strong nuclear force is too strong for the
electric force. In beta decay a neutron in the nucleus of an atom decays
to become a proton and an electron. The proton stays in the nucleus and
the electron flies away at high speed. The electron that flies away is
called a beta particle. The atomic mass number stays the same in beta
decay but the atomic number increases by one unit. A → A and Z
→ (Z + 1). An example reaction looks like this:
14 6C
→ 14 7N
+ 0-1β. It can be
written this way, too: 14 6C
→ 14 7N
+ 0-1e-
A third kind of radioactive decay occurs when there are too many protons in a nucleus for it to be stable (the n0/p+ ratio is too low). In other words, it happens when the electric force is too strong for the strong nuclear force. This kind of decay can happen in two different ways.
First, positron or beta-plus (β+) decay results
in the emission of a positron from within the nucleus. A positron is a
particle that has the same mass as an electron but has a positive charge.
It is the antimatter twin of the electron. The process in the nucleus for
beta-plus decay is that a proton decays to become a neutron and a
positron. The positron flies out of the nucleus and the neutron stays
behind. The atomic mass number stays the same in beta-plus (positron)
decay but the atomic number decreases by one unit. A → A and
Z → (Z - 1). An example reaction looks like this:
2312Mg
→ 2311Na +
0+1β.
It can be written this way, too: 2312Mg →
2311Na
+ 0+1e+.
Second, electron capture can also occur when there are
too many protons in the nucleus of an atom. In this decay mode an electron
that was orbitting the nucleus is absorbed by a proton. The proton is
changed into a neutron as a result and the atomic mass number stays the
same in electron capture decay but the atomic number decreases by one
unit. A → A and Z → (Z - 1). An example reaction looks like
this:
8136Kr
+ 0-1e →
8135Br.
Notice that the electron is added to the
nucleus—nothing is emitted!
The size of an atomic nucleus is unimaginably small. The radius of the
nucleus of a carbon-12 atom is
2.7 × 10-15 m. The radius
of the outermost electron’s orbit in the same atom is about 7.7
× 10-11 m. The volume of that nucleus can be calculated by
treating it as a sphere: the volume of a sphere is V =
4/3πr3. According to this the volume of a carbon-12
nucleus is about 8.69 × 10-44 m3 which is 8.69
× 10-38 cm3. Doing the same thing with the
radius of the atom’s electrons you find a volume of 1.91 ×
10-24 cm3. This is a difference of a factor of 2.2
× 1013! The volume of the nucleus of an atom compared to
the rest of the atom is like a marble compared to a giant sports
stadium.
The nucleus of an atom is extremely dense. The mass of a single carbon-12 nucleus is 1.99 × 10-23 g. So the density of the nucleus is (1.99 × 10-23 g)/(8.69 × 10-38 cm3) = 2.29 × 1014 g/cm3! By contrast, the density of common graphite (a form of carbon) is about 2.2 g/cm3. So the volume of atoms is mostly empty space!
What if you could compress ordinary matter to the same density as the
nuclei of atoms? How big would you be if you were compressed that much?
Find your mass in grams and use the density of a carbon-12 nucleus to find
your new volume. Could you fit in a pocket? Your teacher’s mass is
about 8.6 × 104 g so his volume if all the empty space
were squeezed out of his atoms would be (8.6 × 104 g)
× (1 cm3/2.29 × 1014 g) =
3.76 × 10-10 cm3. This is literally too small
to see!
Answer questions with complete sentences, when appropriate.
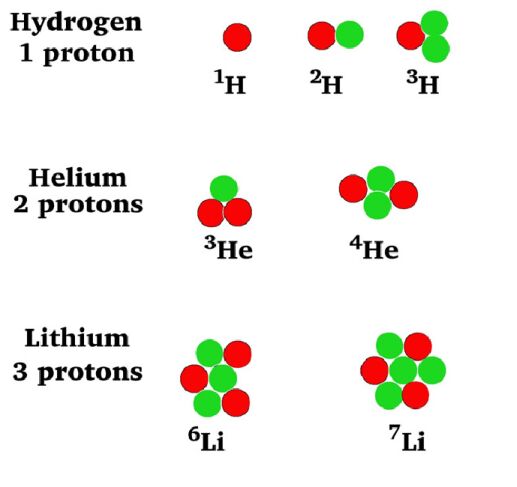 Fill in the
following table with the required information about the isotopes in the
picture at left.
Fill in the
following table with the required information about the isotopes in the
picture at left.
| Name | Symbol | p+ | n0 | Mass |
| hydrogen-1 | 1 1H | 1 | 0 | 1 |
| hydrogen-2 | 2 1H | |||